Group Inverse of 2 × 2 Block Matrices over Minkowski Space M
Vol.06No.03(2016), Article ID:71655,13 pages
10.4236/alamt.2016.63009
Dandapany Krishnaswamy, Tasaduq Hussain Khan
Department of Mathematics, Annamalai University, Annamalai Nagar, India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 1, 2016; Accepted: September 27, 2016; Published: September 30, 2016
ABSTRACT
Necessary and sufficient conditions for the existence of the group inverse of the block matrix 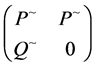 in Minkowski Space are studied, where
in Minkowski Space are studied, where  are both square and
are both square and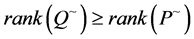 . The representation of this group inverse and some related additive results are also given.
. The representation of this group inverse and some related additive results are also given.
Keywords:
Block Matrix, Group Inverse, Minkowski Adjoint, Minkowski Space

1. Introduction
Let F be a skew field and  be the set of all matrices over F. For
be the set of all matrices over F. For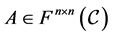 , the matrix
, the matrix 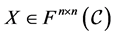 is said to be the group inverse of A, if
is said to be the group inverse of A, if
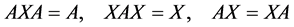 .
.
and is denoted by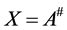 , and is unique by [1] .
, and is unique by [1] .
The generalized inverse of block matrix has important applications in statistical probability, mathematical programming, game theory, control theory etc. and for references see [2] [3] [4] . The research on the existence and the representation of the group inverse for block matrices in Euclidean space has been done in wide range. For the literature of the group inverse of block matrix in Euclidean space, see [5] - [11] .
In [12] the existence of anti-reflexive with respect to the generalized reflection anti- symmetric matrix 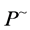 and solution of the matrix equation
and solution of the matrix equation 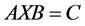 in Minkowski space
in Minkowski space  is given. In [13] necessary and sufficient condition for the existence of Re-nnd solution has been established of the matrix equation
is given. In [13] necessary and sufficient condition for the existence of Re-nnd solution has been established of the matrix equation  where
where 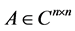 and
and . In [14] partitioned matrix
. In [14] partitioned matrix  in Minkowski space
in Minkowski space 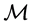 was
was
taken of the form  to yield a formula for the inverse of
to yield a formula for the inverse of 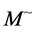
in terms of the Schur complement of .
.
In this paper  and
and  denote the conjugate transpose and Minkowski adjoint of a matrix P respectively.
denote the conjugate transpose and Minkowski adjoint of a matrix P respectively.  denotes the identity matrix of order
denotes the identity matrix of order . Minkowski Space
. Minkowski Space  is an indefinite inner product space in which the metric matrix associated with the indefinite inner product is denoted by G and is defined as
is an indefinite inner product space in which the metric matrix associated with the indefinite inner product is denoted by G and is defined as
 satisfying
satisfying  and
and .
.
G is called the Minkowski metric matrix. In case , indexed as
, indexed as , G is called the Minkowski metric tensor and is defined as
, G is called the Minkowski metric tensor and is defined as  [12] . For any
[12] . For any , the Minkowski adjoint of P denoted by
, the Minkowski adjoint of P denoted by  is defined as
is defined as  where
where  is the usual Hermitian adjoint and G the Minkowski metric matrix of order n. We establish the necessary and sufficient condition for the existence
is the usual Hermitian adjoint and G the Minkowski metric matrix of order n. We establish the necessary and sufficient condition for the existence
and the representation of the group inverse of a block matrix  or
or 
in Minkowski space, where . We also give a sufficient condition for
. We also give a sufficient condition for  to be similar to
to be similar to .
.
2. Lemmas
Lemma 1. Let . If
. If
 ,
,
then there are unitary matrices  such that
such that

where  and
and .
.
Proof. Since  there are two unitary matrices
there are two unitary matrices  such that
such that

where
 .
.
Now

and

From  we have
we have

and from  we get
we get

So,

Lemma 2. Let
 .
.
Then the group inverse of M exists in  if and only if the group inverse of
if and only if the group inverse of 
exists in  and
and . If the group inverse of
. If the group inverse of  exists in M,
exists in M,
then

Proof. Since , suppose group inverse of
, suppose group inverse of  exists in
exists in  and
and . Now
. Now
 .
.
But  because
because  exists
exists . There-
. There-
fore  exists in
exists in .
.
Conversely, suppose the group inverse of M exists in , then it satisfies the following conditions: 1)
, then it satisfies the following conditions: 1)  2)
2)  and 3)
and 3) . Also
. Also
 .
.
Let  then,
then,
1)

2)

3)

Lemma 3. Let , and
, and . Then the
. Then the
group inverse of M exists in  if and only if the group inverse of
if and only if the group inverse of  exists in
exists in  and
and . If the group inverse of M exists in
. If the group inverse of M exists in , then,
, then,

Proof. The proof is same as Lemma 2.
Lemma 4. Let . If
. If

then the following conclusions hold:
1) 
2) 
3) 
4) 
5) 
Proof. Suppose , then by Lemma 1 we have
, then by Lemma 1 we have

where . Then
. Then

Since  we have that
we have that  is invertible. By using Lemma 2 and 3 we get
is invertible. By using Lemma 2 and 3 we get

Then, 1)

Similarly we can prove 2) - 5).
3. Main Results
Theorem 1. Let  where
where , then
, then
1) The group inverse of M exists in  if and only if
if and only if
 .
.
2) If the group inverse of M exists in , then
, then , where
, where

Proof. 1) Given . Suppose
. Suppose  then,
then,
 . We know that
. We know that
 so,
so, .
.
Therefore the group inverse of M exists. Now we show that the condition is ne- cessary,

 .
.
Since the group inverse of M exists in  if and only if
if and only if , we have
, we have

Also

Then  and
and . Therefore,
. Therefore,
 .
.
From

and
 ,
,
we have

Since

and
 ,
,
we get
 .
.
Thus
 .
.
Then there exists a matrix  such that
such that . Then
. Then
 .
.
So, we get
 .
.
2) Let , we will prove that the matrix X satisfies the conditions of
, we will prove that the matrix X satisfies the conditions of
the group inverse in . Firstly we compute
. Firstly we compute


Applying Lemma 4 1), 2) and 5) we have
















Now




 □
□
Theorem 2. Let  in
in , where
, where ,
,

Then,
1) the group inverse of M exists in  if and only if
if and only if
 .
.
2) if the group inverse of M exists in , then
, then , where
, where

Proof. 1) Given . Suppose
. Suppose  then,
then,
 .
.
We know that

so,
 .
.
Therefore the group inverse of M exists in . Now we show that the condition is necessary,
. Now we show that the condition is necessary,



Since the group inverse of M exists in  if and only if
if and only if . We know
. We know

Also

Then  and
and  Therefore
Therefore

From

and

we have

Since

and
 ,
,
we get
 .
.
Thus

Then there exist a matrix  such that
such that  Thus
Thus

So, we get .
.
2) Proof is same as Theorem 1 2).
Theorem 3. Let  if
if
 .
.
Then  and
and  are similar.
are similar.
Proof. Suppose , then by using Lemma 1, there are unitary matrices
, then by using Lemma 1, there are unitary matrices  such that
such that
 ,
, 
where . Hence
. Hence


So  and
and  are similar.
are similar.
Cite this paper
Krishnaswamy, D. and Khan, T.H. (2016) Group Inverse of 2 ´ 2 Block Matrices over Minkowski Space M. Ad- vances in Linear Algebra & Matrix Theory, 6, 75-87. http://dx.doi.org/10.4236/alamt.2016.63009
References
- 1. Zhuang, W. (1987) Involutory Functions and Generalized Inverses of Matrices over an Arbitrary Skew Fields. Northeast Math, 1, 57-65.
- 2. Golub, G.H. and Greif, C. (2003) On Solving Blocked-Structured Indefinite Linear Systems. SIAM Journal on Scientific Computing, 24, 2076-2092.
- 3. Ipsen, I.C.F. (2001) A Note on Preconditioning Nonsymmetric Matrices. SIAM Journal on Scientific Computing, 23, 1050-1051.
- 4. Campbell, S.L. and Meyer, C.D. (2013) Generalized Inverses of Linear Transformations. Dover, New York.
- 5. Bu, C. (2002) On Group Inverses of Block Matrices over Skew Fields. Journal of Mathematics, 35, 49-52.
- 6. Bu, C., Zhao, J. and Zheng, J. (2008) Group inverse for a Class 2 × 2 Block Matrices over Skew Fields. Computers & Mathematics with Applications, 204, 45-49.
http://dx.doi.org/10.1016/j.amc.2008.05.145 - 7. Cao, C. (2001) Some Results of Group Inverses for Partitioned Matrices over Skew Fields. Heilongjiang Daxue Ziran Kexue Xuebao, 18, 5-7.
- 8. Cao, C. and Tang, X. (2006) Representations of the Group Inverse of Some 2 × 2 Block Matrices. International Mathematical Forum, 31, 1511-1517.
http://dx.doi.org/10.12988/imf.2006.06127 - 9. Chen, X. and Hartwig, R.E. (1996) The Group Inverse of a Triangular Matrix. Linear Algebra and Its Applications, 237/238, 97-108.
http://dx.doi.org/10.1016/0024-3795(95)00561-7 - 10. Catral, M., Olesky, D.D. and van den Driessche, P. (2008) Group Inverses of Matrices with Path Graphs. The Electronic Journal of Linear Algebra, 1, 219-233.
http://dx.doi.org/10.13001/1081-3810.1260 - 11. Cao, C. (2006) Representation of the Group Inverse of Some 2 × 2 Block Matrices. International Mathematical Forum, 31, 1511-1517.
- 12. Krishnaswamy, D. and Punithavalli, G. (2013) The Anti-Reflexive Solutions of the Matrix Equation A × B=C in Minkowski Space M. International Journal of Research and Reviews in Applied Sciences, 15, 2-9.
- 13. Krishnaswamy, D. and Punithavalli, G. (2013) The Re-nnd Definite Solutions of the Matrix Equation A × B=C in Minkowski Space M. International Journal of Fuzzy Mathematical Archive, 2, 70-77.
- 14. Krishnaswamy, D. and Punithavalli, G. Positive Semidefinite (and Definite) M-Symmetric Matrices Using Schur Complement in Minkowski Space M. (Preprint)
上一篇:Jordan Γ*-Derivation on 下一篇:On Characterization of Poised
最新文章NEWS
- On Characterization of Poised Nodes for a Space of Bivariate Functions
- Least-Squares Solutions of Generalized Sylvester Equation with Xi Satisfies Different Linear Constra
- Matrices and Division by Zero z/0 = 0
- Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution
- Two Nonzero Component Lemma and Matrix Trigonometry
- Using Row Reduced Echelon Form in Balancing Chemical Equations
- Tight Monomials with t-Value ≤ 9 for Quantum Group of Type D4
- Minimum Covering Randić Energy of a Graph
推荐期刊Tui Jian
- Chinese Journal of Integrative Medicine
- Journal of Genetics and Genomics
- Journal of Bionic Engineering
- Pedosphere
- Chinese Journal of Structural Chemistry
- Nuclear Science and Techniques
- 《传媒》
- 《哈尔滨师范大学自然科学学报》
热点文章HOT
- Using Row Reduced Echelon Form in Balancing Chemical Equations
- Minimum Covering Randić Energy of a Graph
- A Note on the Inclusion Sets for Tensors
- A General Hermitian Nonnegative-Definite Solution to the Matrix Equation AXB = C
- Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution
- Matrices and Division by Zero z/0 = 0
- On Characterization of Poised Nodes for a Space of Bivariate Functions
- Pseudo Laguerre Matrix Polynomials, Operational Identities and Quasi-Monomiality
