ABSTRACT

In an earlier paper published in the Journal of Natural Sciences Research in 2015 on how to balance chemical equations using matrix algebra, Gabriel and Onwuka showed how to reduce the resulting matrix to echelon form using elementary row operations. However, they did not show how elementary row operations can be used in reducing the resulting echelon matrix to row reduced echelon form. We show that the solution obtained is actually the nullspace of the matrix. Hence, the solution can be infinitely many. In addition, we show that instead of manually using row operations to reduce the matrix to row reduced echelon form, software environments like octave or Matlab can be used to reduce the matrix directly. In all the examples presented in this paper, we reduced all matrices to row reduced echelon form showing all row operations, which was not clearly stated in the Gabriel and Onwuka paper. Most importantly, with the availability of Mathematical software, we show that we do not need to carry out these row operations by brute force.

Keywords:

Nullspace, Chemical Equations

1. Introduction

According to Risteski [1] , a chemical reaction is an expression showing a symbolic re- presentation of the reactants and products that is usually positioned on the left and right hand sides of a particular chemical reaction. Substances that takes part in a che- mical reaction are represented by their molecular formula and their symbolic repre- sentation is also regarded as a chemical reaction [2] . A chemical reaction can either be reversible or irreversible. These differs from Mathematical equations in the sense that while a single arrow (in the case of an irreversible reaction) or a double arrow points in the forward and backward directions of both the reactants and products (in the case of a reversible reaction) connects chemical reactions [3] , an equality sign links the left and right hand sides of a Mathematical equation. “The quantitative and qualitative know- ledge of the chemical processes which estimates the amount of reactants, predicting the nature and amount of products and determining conditions under which a reaction takes place is important in balancing a chemical reaction. Balancing Chemical reaction is an excellent demonstative and instructive example of the inter-connectedness be- tween Linear Algebra and Stoichiometric principles” [4] .

If the number of atoms of each type of element on the left is the same as the number of atoms of the corresponding type on the right, then the chemical equation is said to be balanced [3] , otherwise it is not. The qualitative study of the relationship between reactants in a chemical reaction is termed Stoichiometry [5] . Tuckerman [6] mentioned two methods for balancing a Chemical reaction: by inspection and algebraic. The ba- lancing-by-inspection method involves making successive intelligent guesses at making the coefficients that will balance an equation equal and continuing until the equation is balanced [4] . For simple equations, this procedure is straight forward. However, according to [7] , there is need for a “step-by-step” approach which is easily applicable and can be mastered; rather than the haphazard hoping of inspection or a highly refined inspection. In addition, balancing-by-inspection method makes one to believe that there is only one possible solution rather than an infinite number of solutions which the method proposed in this paper illustrates. The algebraic approach circumvents the above loo- pholes provided in the inspection method and can handle complex chemical reac- tions.

The algebraic approach discussed in [6] , involves putting unknown coefficients in front of each molecular species in the equation and solving for the unknowns. This is then followed by writing down the balance conditions on each element. After which he lets one of the unknowns to be one and takes turns to obtain the coefficients of the remaining unknowns. In the proposed approach, instead of setting one of the unknowns to zero, we write out the set of equations in matrix form, obtain a homogeneous system of equations. Since the system of equations is homogeneous, the solution obtained is in the nullspace of the corresponding matrix. We then perform elementary row operations on the matrix to reduce it to row reduced echelon form. We also show the use of software environments like Matlab/octave to reduce the corresponding matrix to row reduced echelon form using the rref command. This approach surpasses those in [4] ; in the sense that we do not need to manually reduce the matrix to echelon form as shown in that paper. In that paper, they showed how the corresponding matrix is reduced to echelon form but did not use elementary row operations to convert it to row reduced echelon form.

In the next section, we state two well known results partaining echelon form and row reduced echelon form.

2. Methodolology

In this section, we state well known results about echelon form and row reduced echelon form. We will not bother about the algorithm as this is readily available in most Linear Algebra textbooks.

Lemma 2.1.: The number of nonzero rows and columns are the same in any echelon form produced from a given matrix 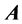by elementary row operations, irrespective of the sequence of row operations used.

Given an 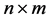matrix,

1. Use Gauss elimination to produce an echelon form from.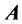

2. Use the bottom-most non zero entry in each leading column of the echelon form, starting with the rightmost leading column and working to the left, so as to eliminate all non-zero entries in that column strictly above that entry one.

Definition 2.1 An matrix 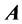is said to be in row reduced echelon from when:

1. It is in echelon form (with non-zero rows, say)

2. The 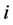th leading column equals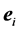, the 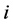th column of the identity matrix of orde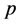r, for.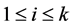

The next result which can be found in [8] , describes the uniqueness of the row reduced echelon form. It is the uniqueness of the row reduced echelon form that makes it a tool for finding the nullspace of a matrix.

Theorem 2.1 (Row Reduced Echelon Form): Each matrix has precisely one row reduced echelon form to which it can be reduced by elementary row operations, regardless of the actual sequence of operations used to produce it.

Proof. See [8] .

3. Worked Examples

Example 3.1.: Rust is formed when there is a chemical reaction between iron and oxygen. The compound that is formed is a reddish-brown scales that cover the iron object. Rust is an iron oxide whose chemical formula is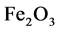, so the chemical for- mula for rust is

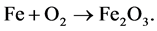
Balance the equation.

In balancing the equation, let 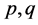and be the unknown variables such that

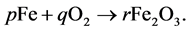
We compare the number of Iron (Fe) and Oxygen (O) atoms of the reactants with the number of atoms of the product. We obtain the following set of equations:

The homogeneous system of equations becomes

From the above, the matrix is already in the echelon form, with two pivots 1 and 2 but not in row reduced echelon form, even though there is a zero above the second pivot 2. However, to reduce it to row reduced echelon form; all the pivots

must be one. Hence, we replace row two with half row two, that is to yield,

(1)

Thus, becomes

Upon expanding, we have

the nullspace solution

There are three pivot variables and one free variable. If we choose, then. To avoid fractions, we can also let, so that and

. We remark that these are not the only solutions since there is a free variable, the nullspace solution is infinitely many. Therefore, the chemical equation can be balanced as

or

Example 3.2.: Ethane burns in oxygen to produce carbon (IV) oxide and steam. The steam condenses to form droplets of water viz;

balance the equation.

Let the unknowns be and, such that

We compare the number of Carbon (C), Hydrogen (H) and Oxygen (O) atoms of the reactants with the number of atoms of the products. We obtain the following set of equations:

In homogeneous form,

In the first step of elimination, replace row two by row two minus three times row one, i.e., to yield,

Exchange row two with row three or vice versa to reduce to echelon form,

In the next set of operations that we will carry out to reduce to, we perform row operations that will change the entries above the pivots to zero; Replace row one by three times row two plus two times row three i.e., and replace row one with three times row one plus row three to yield

The last operation that will give us, is to reduce all the pivots to unity, that is replace row one with one-sixth row one, row two with one-sixth row two and row three with one-third row three to obtain

(2)

The solution to reduces to where is actually the nullspace of which is equivalent to the nullspace of. Hence,

Upon expanding, we have

the nullspace solution

There are three pivot variables and one free variable. Let, so that and. We remark that this is not the only solution since there is a

free variable, the nullspace solution is infinitely many. Therefore, the chemical equation can be balanced as

Example 3.3.: Sodium hydroxide (NaOH) reacts with sulphuric acid to yield sodium sulphate and water,

Balance the equation.

In balancing the equation, let and be the unknown variables such that

We compare the number of Sodium (Na), Oxygen (O), Hydrogen (H) and Sulphur (S) atoms of the reactants with the number of atoms of the products. We obtain the following set of equations:

Re-writing these equations in standard form, we have a homogeneous system of linear equations with and

or

The augmented system becomes

Since the right hand side is the zero vector, we work with the matrix because any row operation will not change the zeros.

Replace row 2 with row two minus row one i.e.,. Similarly, replace row three with row three minus row one i.e.,. These first set of row operations reduces to

In the second set of row operations, we replace row three by two times row three minus row two or and replace row four by four times row four minus row two or to yield

In the third stage of the elimination process, we replace row four with 3 times row four plus row three i.e., to yield the row echelon matrix or upper triangular,

We now reduce to row reduced echelon form as follows: First, we reduce the pivots to unity in rows two and three via and to obtain

Replace row one by row one plus two times row three i.e., and row two by row two plus half row three, that is. These two operations

replaces all nonzeros above the pivots to zero resulting in the row reduced echelon form

(3)

The solution to reduces to where is actually the nullspace of which is equivalent to the nullspace of. Hence,

Upon expanding, we have

the nullspace solution

There are three pivot variables and one free variable. We set, so that and. We remark that this is not the only solution since there is a free variable, the nullspace solution is infinitely many. Therefore, the chemical equation can be '”balanced” as

Example 3.4.: Using row reduced echelon form, balance the following chemical reaction:

Let and be the unknown variables such that

We obtain the following set of equations for each of the elements:

The corresponding matrix becomes

The following row operations, and reduces to

In the same vein, the following row operations and reduces the above matrix to

Finally, reduces the matrix to echelon form

There are three pivots respectively. Hence, to reduce the matrix to row reduced echelon form, we make sure the entries above the pivots are zero and then change the pivots to unity. The row operations, and

changes the nonzero entries above the pivots to zero so that reduces to

The row operations, and leads to the row reduced echelon form

(4)

Therefore, the solution to becomes

For simplicity, we equate to one so that. This actually shows that the equation was balanced in the first place.

4. Using Matlab or Octave rref Command

In this section, we use octave to reduce each of the matrices considered in the last section to row reduced echelon form. We remark that just as predicted by the theory, row exchanges does not change the outcome of row reduced echelon form. This means that if you interchange any of the row of each of the matrices in the four examples, the rref will be the same.

Example 4.1.: Type the matrix and. This gives the same as in (1) as

Example 4.2.: and. This gives the same as in (2) as

Example 4.3.: and . This gives the same as in (3) as

Example 4.4.: and . This gives the same as in (4) as

In the next example, we illustrate the power of the rref command.

Example 4.5.: Consider balancing the following chemical reaction from [6]

Let the unknown coefficients be such that

We write down the balance conditions on each element as

Sodium:.

Chlorine:.

Sulphur:.

Oxygen:.

Hydrogen:

After transposing, the above system of equations can be written in the form as

Using Matlab or Octave command, reduces to as

If we set, then and. The balanced equation be- comes

5. Conclusion

In this paper, we have shown how to balance chemical equations using row reduced echelon form. In actual fact, the echelon form alone could have been used and we still have the same solution but reducing it to rref makes the solution easily deduced. This paper improves on the work of Gabriel and Onwuka and we show that the octave/ Matlab rref command can be used to confirm the correctness of the final output on the one hand or as a stand alone.

Cite this paper

Akinola, R.O., Kut- chin, S.Y., Nyam, I.A. and Adeyanju, O. (2016) Using Row Reduced Echelon Form in Balancing Chemical Equations. Advances in Linear Algebra & Matrix Theory, 6, 146- 157. http://dx.doi.org/10.4236/alamt.2016.64014

References