Least-Squares Solutions of Generalized Sylvester Equation with Xi Satisfies Different Linear Constra
Vol.06No.02(2016), Article ID:67303,16 pages
10.4236/alamt.2016.62008
Xuelin Zhou, Dandan Song, Qingle Yang, Jiaofen Li*
School of Mathematics and Computing Science, Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guilin University of Electronic Technology, Guilin, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 March 2016; accepted 11 June 2016; published 14 June 2016
ABSTRACT
In this paper, an iterative method is constructed to find the least-squares solutions of generalized Sylvester equation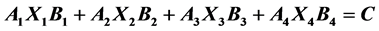 , where
, where 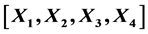 is real matrices group, and
is real matrices group, and 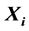 satisfies different linear constraint. By this iterative method, for any initial matrix group
satisfies different linear constraint. By this iterative method, for any initial matrix group 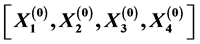 within a special constrained matrix set, a least squares solution group
within a special constrained matrix set, a least squares solution group 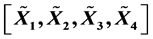 with
with 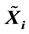 satisfying different linear constraint can be obtained within finite iteration steps in the absence of round off errors, and the unique least norm least-squares solution can be obtained by choosing a special kind of initial matrix group. In addition, a minimization property of this iterative method is characterized. Finally, numerical experiments are reported to show the efficiency of the proposed method.
satisfying different linear constraint can be obtained within finite iteration steps in the absence of round off errors, and the unique least norm least-squares solution can be obtained by choosing a special kind of initial matrix group. In addition, a minimization property of this iterative method is characterized. Finally, numerical experiments are reported to show the efficiency of the proposed method.
Keywords:
Least-Squares Problem, Centro-Symmetric Matrix, Bisymmetric Matrix, Iterative Method

1. Introduction
A matrix  is said to be a Centro-symmetric matrix if
is said to be a Centro-symmetric matrix if  for all
for all . A matrix
. A matrix 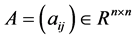 is said to be a Bisymmetric matrix if
is said to be a Bisymmetric matrix if 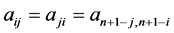 for all
for all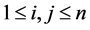 . Let
. Let
 and
and 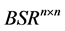 denote the set of
denote the set of 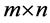 real matrices,
real matrices,  real symmetric matrices,
real symmetric matrices,  real Centro-symmetric matrices and
real Centro-symmetric matrices and  real Bisymmetric matrices, respectively.
real Bisymmetric matrices, respectively.  where
where  denotes ith column of
denotes ith column of  unit matrix. For a matrix
unit matrix. For a matrix , we denote its transpose, traced by
, we denote its transpose, traced by  respectively. In space
respectively. In space , we define inner product as:
, we define inner product as:  for all
for all , then the norm of a matrix A generated by this inner product is, obviously, Frobenius norm and denoted by
, then the norm of a matrix A generated by this inner product is, obviously, Frobenius norm and denoted by .
.
Denote

Obviously, K, i.e. , is a linear subspace of real number field.
, is a linear subspace of real number field.
In this paper, we mainly consider the following two problems:
Problem I. Given matrices ,
, 
 , find matrix group
, find matrix group  such that
such that

Problem II. Denote by  the solution set of Problem I. Find matrix group
the solution set of Problem I. Find matrix group , such that
, such that

In fact, Problem II is to find the least norm solution of Problem I.
There are many valuable efforts on formulating solutions of various linear matrix equations with or without linear constraint. For example, Baksalary and Kala [1] , Chu [2] [3] , Peng [4] , Liao, Bai and Lei [5] and Xu, Wei and Zheng [6] considered the nonsymmetric solution of the matrix equation
 (1)
(1)
by using Moore-Penrose generalized inverse and the generalized singular value decomposition of matrices, while Chang and Wang [7] considered the symmetric conditions on the solution of the matrix equations
 (2)
(2)
Zietak [8] [9] discussed the  -solution and Chebyshev-solution of the matrix equation
-solution and Chebyshev-solution of the matrix equation
 (3)
(3)
Peng [10] researched the general linear matrix equation
 (4)
(4)
with the bisymmetric conditions on the solutions. Vec operator and Kronecker product are employed in this paper, so the size of the matrix is enlarged greatly and the computation is very expensive in the process of solving solutions. Iterative algorithms have been received much attention to solve linear matrix equations in recent years. For example, by extending the well-known Jacobi and Gauss-seidel iterations for , Ding, Liu and Ding in [11] derived iterative solutions of matrix equations
, Ding, Liu and Ding in [11] derived iterative solutions of matrix equations  and generalized Sylvester matrix equations
and generalized Sylvester matrix equations . By absorbing the thought of the conjugate gradient method, Peng [12] presented an iterative algorithm to solve Equation (1). Peng [13] , Peng, Hu and Zhang [14] put forward an iterative method for bisymmetric solution of Equation (4). These matrix-form CG methods are based on short recurrences, which keep work and storage requirement constant at each iteration. However, these iteration methods are only defined by the Galerkin condition, but lack of a minimization property, which means that the algorithm may exhibit a rather irregular convergence, and often results in a very slow convergence. Lei and Liao [15] presented that a minimal residual algorithm could remedy this problem, and this algorithm satisfies a minimization property, which ensures that this method possesses a smoothly convergence.
. By absorbing the thought of the conjugate gradient method, Peng [12] presented an iterative algorithm to solve Equation (1). Peng [13] , Peng, Hu and Zhang [14] put forward an iterative method for bisymmetric solution of Equation (4). These matrix-form CG methods are based on short recurrences, which keep work and storage requirement constant at each iteration. However, these iteration methods are only defined by the Galerkin condition, but lack of a minimization property, which means that the algorithm may exhibit a rather irregular convergence, and often results in a very slow convergence. Lei and Liao [15] presented that a minimal residual algorithm could remedy this problem, and this algorithm satisfies a minimization property, which ensures that this method possesses a smoothly convergence.
However, to our best knowledge, the unknown matrix with different linear constraint of linear matrix equations, such as Equations ((1)-(4)), has not been considered yet. No loss of generality, we research the following case
 (5)
(5)
which has four unknown matrices and each is required to satisfy different linear constraint. We should point out that the matrices  are experimentally occurring in practices, so they may not satisfy solvability conditions. Hence, we should study the least squares solutions, i.e. Problem I. Noting that it is obvious difficulties to solve this problem by conventional methods, such as matrix decomposition and ver operator, hence iterative method is considered. Absorbing the thought of the minimal residual algorithm presented by Lei and Liao [15] , and combing the trait of problem, we conduct an iterative method for solving Problem I. This method can both maintain the short recurrence and satisfy a minimization property, i.e. the approximation solution minimizes the residual norm of Equation (5) over a special affine subspace, which ensures that this method converges smoothly.
are experimentally occurring in practices, so they may not satisfy solvability conditions. Hence, we should study the least squares solutions, i.e. Problem I. Noting that it is obvious difficulties to solve this problem by conventional methods, such as matrix decomposition and ver operator, hence iterative method is considered. Absorbing the thought of the minimal residual algorithm presented by Lei and Liao [15] , and combing the trait of problem, we conduct an iterative method for solving Problem I. This method can both maintain the short recurrence and satisfy a minimization property, i.e. the approximation solution minimizes the residual norm of Equation (5) over a special affine subspace, which ensures that this method converges smoothly.
The paper is organized as follows. In Section 2, we first conduct an iterative method for solving Problem I, and then describe the basic properties of this method; we also solve Problem II by using this iterative method. In Section 3, we show that the method possesses a minimization property. In Section 4, we present numerical experiments to show the efficiency of the proposed method, and use some conclusions in Section 5 to end our paper.
2. The Iterative Method for Solving Problem I and II
In this section, we firstly introduce some lemmas which are required for solving Problem I, we then conduct an iterative method to obtain the solution of Problem I. We show that, for any initial matrix group  , the matrix group sequences
, the matrix group sequences  generated by the iterative method converge to a solution of Problem I within finite iteration steps in the absence of roundoff errors. We also show that the unique least norm solution of Problem I can be obtained by choosing a special kind of initial matrix group.
generated by the iterative method converge to a solution of Problem I within finite iteration steps in the absence of roundoff errors. We also show that the unique least norm solution of Problem I can be obtained by choosing a special kind of initial matrix group.
Lemma 1. [16] [17] . A matrix  if and only if
if and only if .
.
A matrix  if and only if
if and only if .
.
Lemma 2. Suppose that a matrix , then
, then .
.
Suppose that a matrix , then
, then .
.
Proof: Its proof is easy to obtain from Lemma 1. W
Lemma 3. Suppose that ,
,  ,
,  ,
,  then
then

Proof: It is easy to verify from direct computation. W
Lemma 4. (Projection Theorem) [18] . Let X be a finite dimensional inner product space, M be a subspace of X, and  be the orthogonal complement subspace of M. For a given
be the orthogonal complement subspace of M. For a given , there always exists an
, there always exists an  such that
such that

where  is the norm associated with the inner product defined in X. Moreover,
is the norm associated with the inner product defined in X. Moreover,  is the unique minimization vector in M if and only if
is the unique minimization vector in M if and only if

Lemma 5. Suppose  is the residual of matrix group
is the residual of matrix group  corresponding to Equation (5), i.e.
corresponding to Equation (5), i.e. , if the following conditions are satisfied simultaneously,
, if the following conditions are satisfied simultaneously,
 (6)
(6)
then the matrix group  is a solution of Problem I.
is a solution of Problem I.
Proof: Let

obviously, Z is a linear subspace of . For matrix group
. For matrix group , denote
, denote

then . Applying to Lemma 4, we know that
. Applying to Lemma 4, we know that  is a solution of Problem I if and only if
is a solution of Problem I if and only if

i.e. for all ,
,

By Lemma 3, it is easy to verify that if the equations of (6) are satisfied simultaneously, the expression above holds, which means  is a solution of Problem I. W
is a solution of Problem I. W
Lemma 6. Suppose that matrix group  is a solution of Problem I, then arbitrary matrix group
is a solution of Problem I, then arbitrary matrix group  can be express as
can be express as  where matrix group
where matrix group  satisfies
satisfies
 (7)
(7)
Proof: Assume that matrix group  is a solution of Problem I. If
is a solution of Problem I. If  , then by Lemma 5 and its proof process, we have
, then by Lemma 5 and its proof process, we have

which implies matrix group  satisfies (7).
satisfies (7).
Conversely, if matrix group

where matrix group  satisfies (7), then
satisfies (7), then

which means matrix group  W
W
Next, we develop iterative algorithm for the least-squares solutions with  satisfies different linear constraint of matrix equation
satisfies different linear constraint of matrix equation

where ,
,  and C are given constant matrices, and
and C are given constant matrices, and  is the unknown matrices group to be solved.
is the unknown matrices group to be solved.
Algorithm 1. For an arbitrary initial matrix group , compute
, compute
Step 1. 

Step 2. If , then stop; else,
, then stop; else,  , and compute
, and compute
Step 3. 

Step 4. Go to step 2.
Remark 1. 1) Obviously, matrices sequence  generated by Algorithm 1 satisfies
generated by Algorithm 1 satisfies

2)  is the residual of Equation (5), when
is the residual of Equation (5), when 
3) Algorithm 1 implies that if , then the corresponding matrix group
, then the corresponding matrix group  is the solution of Problem I.
is the solution of Problem I.
In the next part, we will show the basic properties of iteration method by induction. First for convenience of discussion in the later context, we introduce the following conclusions from Algorithm 1. For all 

Lemma 7. For matrices ,
,  (r = 1, 2, 3, 4) and
(r = 1, 2, 3, 4) and  generated by Algorithm 1, if there exist a positive integer k such that
generated by Algorithm 1, if there exist a positive integer k such that ,
,  , and
, and  for all
for all , then we have
, then we have
1) 
2) 
3) 
Proof: For , it follows that
, it follows that



Assume that the conclusions

hold for all , then
, then



By the assumption of Equation (3), we have

Then for j = s,



Then the conclusion  and the assumption
and the assumption  show that
show that
 for all
for all . By the principal of induction, we know that Eq.(3) holds for all
. By the principal of induction, we know that Eq.(3) holds for all , and Equation (1) and Equation (2) hold for all
, and Equation (1) and Equation (2) hold for all  due to the fact that
due to the fact that  holds for all matrices A and B in
holds for all matrices A and B in . W
. W
Lemma 7. shows that the matrix sequence

generated by Algorithm 1 are orthogonal each other in the finite dimension matrix space . Hence the iterative method will be terminated at most
. Hence the iterative method will be terminated at most  steps in the absence of roundoff errors.
steps in the absence of roundoff errors.
It is worth to note that the conclusions of Lemma 7 may not be true without the assumptions  and
and . Hence it is necessary to consider the case that
. Hence it is necessary to consider the case that  or
or .
.
If , which implies
, which implies , it follows that
, it follows that .
.
If , which implies
, which implies , then we have
, then we have , making inner product with
, making inner product with  by both side, yields
by both side, yields

So the discussions above show that if there exist a positive integer i such that the coefficient  or
or , then the corresponding matrix group
, then the corresponding matrix group  is just the solution of Problem I.
is just the solution of Problem I.
Together with Lemma 7 and the discussion about the coefficient , we can conclude the following theorem.
, we can conclude the following theorem.
Theorem 1. For an arbitrary initial matrix group , the matrix group sequence
, the matrix group sequence  generated by Algorithm 1 will converge to a solution of Problem I at infinite iteration steps in exact arithmetic.
generated by Algorithm 1 will converge to a solution of Problem I at infinite iteration steps in exact arithmetic.
By choosing a special kind of initial matrix group, we can obtain the unique least norm of Problem I. To this end, we first define a matrix set as follows

where . Evidently, S is a linear subspace of K.
. Evidently, S is a linear subspace of K.
Theorem 2. If we choose the initial matrix group , especially, let
, especially, let  , we can obtain the least norm solution of Problem I.
, we can obtain the least norm solution of Problem I.
Proof: By the Algorithm 1 and Theorem 1, if we choosing initial matrix group , we can obtain the solution
, we can obtain the solution  of Problem I with finite iteration steps and there exist a matrix
of Problem I with finite iteration steps and there exist a matrix  such that the solution
such that the solution  can be represented that
can be represented that

By Lemma 6 we know that arbitrary solution of Problem I can be express as

where matrix group  satisfies (7).
satisfies (7).
Then

So we have

which implies that matrix group  is the least norm solution of Problem I. W
is the least norm solution of Problem I. W
Remark 2. Since the solution of Problem I is no empty, so the  is a closed convex linear subspace, hence it is certain that the least norm solution group
is a closed convex linear subspace, hence it is certain that the least norm solution group  of Problem I is unique, and
of Problem I is unique, and  . If matrix group
. If matrix group  is a solution of Problem I, then it just be the unique least norm solution of Problem I, i.e.
is a solution of Problem I, then it just be the unique least norm solution of Problem I, i.e. .
.
3. The Minimization Property of Iterative Method
In this section, the minimization property of Algorithm 1 is characterized, which ensures the Algorithm 1 converges smoothly.
Theorem 3. For an arbitrary initial matrix group , the matrix group
, the matrix group  generated by Algorithm 1 at the kth iteration step satisfies the following minimization problem
generated by Algorithm 1 at the kth iteration step satisfies the following minimization problem

where F denote a affine subspace which has the following form

Proof: For arbitrary matrix group , there exist a set of real number
, there exist a set of real number  such that
such that

Denote

by the conclusion Equation (2) in Lemma 7, we have

where  is the corresponding residual of initial matrix group
is the corresponding residual of initial matrix group . Algorithm 1 show that the matrix
. Algorithm 1 show that the matrix  can be express as
can be express as

Because  is a continuous and differentiable function with respect to the k variable
is a continuous and differentiable function with respect to the k variable  , we easily know that
, we easily know that

if and only if

It follows from the conclusion in Lemma 7 that

By the fact that

We complete the proof. W
Theorem 3 shows that the approximation solution  minimizes the residual norm in the affine subspace F for all initial matrix group within K. Furthermore, by the fact
minimizes the residual norm in the affine subspace F for all initial matrix group within K. Furthermore, by the fact
 , then we have
, then we have

which shows that the sequence

is monotonically decreasing. The descent property of the residual norm of Equation (5) ensures that the Algorithm 1 possesses fast and smoothly convergence.
4. Numerical Examples
In this section, we present numerical examples to illustrate the efficiency of the proposed iteration method. All the tests are performed using Matlab 7.0 which has a machine precision of around 10−16. Because of the error of calculation, the iteration will not stop within finite steps. Hence, we regard the approximation solution group
 as the solution of Problem I if the corresponding
as the solution of Problem I if the corresponding  satisfies
satisfies .
.
Example 1. Given matrices  and C as follows:
and C as follows:






Choose the initial matrices  where 0 denotes zero matrix in appropriate dimension. Using Algorithm 1 and iterating 74 steps, we have the unique least norm solution
where 0 denotes zero matrix in appropriate dimension. Using Algorithm 1 and iterating 74 steps, we have the unique least norm solution  as follows:
as follows:




with

And

If we let the initial matrix , noting that
, noting that  within K but not within S, then we have
within K but not within S, then we have




with

And

Example 2. Suppose that the matrices  are the same as Example 1, let
are the same as Example 1, let  , where
, where ,
,  ,
,  ,
,  , that is to say, Equation (5) is consistent over set K. Then similarly Algorithm 2.1 in Peng [14] we can conduct another iteration algorithm as follows:
, that is to say, Equation (5) is consistent over set K. Then similarly Algorithm 2.1 in Peng [14] we can conduct another iteration algorithm as follows:
Algorithm 2. For an arbitrary initial matrix group , compute
, compute
Step 1. 

Step 2. If , then stop; else,
, then stop; else,  , and compute
, and compute
Step 3. 

Step 4. Go to step 2.
The main differences of Algorithm 1 and Algorithm 2 are: in Algorithm 1 the selection of coefficient  make
make , and
, and  such that
such that  but in Algorithm 2, the choosing of
but in Algorithm 2, the choosing of  such that
such that , and
, and  such that
such that . Noting that Algorithm 2 satisfies
. Noting that Algorithm 2 satisfies
the Galerkin condition, but lacks of minimization property. Choosing the initial matrix  where 0 denotes zero matrix in appropriate dimension, by making use of Algorithm 1 and Algorithm 2, we can
where 0 denotes zero matrix in appropriate dimension, by making use of Algorithm 1 and Algorithm 2, we can

Figure 1. The comparison of residual norm between these two algorithm.
obtain the same least norm solution group, and we also obtain the convergence curves of residual norm shown in Figure 1. The results in this figure show clearly that the residual norm of Algorithm 1 is monotonically decreasing, which is in accordance with the theory established in this paper, and the convergence curve is more smooth than that in Algorithm 2.
Acknowledgements
We thank the Editor and the referee for their comments. Research supported by the National Natural Science Foundation of China (11301107, 11261014, 11561015, 51268006).
Cite this paper
Xuelin Zhou,Dandan Song,Qingle Yang,Jiaofen Li, (2016) Least-Squares Solutions of Generalized Sylvester Equation with Xi Satisfies Different Linear Constraint. Advances in Linear Algebra & Matrix Theory,06,59-74. doi: 10.4236/alamt.2016.62008
References
- 1. Baksalary, J.K. and Kala, R. (1980) The Matrix Equation AXB+CYD=E. Linear Algebra and Its Applications, 30, 141-147.
http://dx.doi.org/10.1016/0024-3795(80)90189-5 - 2. Chu, K.E. (1987) Singular Value and Generlized Value Decompositions and the Solution of Linear Matrix Equations. Linear Algebra and Its Applications, 87, 83-98.
http://dx.doi.org/10.1016/0024-3795(87)90104-2 - 3. Chu, K.E. (1989) Symmetric Solutions of Linear Matrix Equation by Matrix Decompositions. Linear Algebra and Its Applications, 119, 35-50.
http://dx.doi.org/10.1016/0024-3795(89)90067-0 - 4. Peng, Z.Y. (2002) The Solutions of Matrix AXC+BYD=E and Its Optimal Approximation. Mathematics: Theory & Applications, 22, 99-103.
- 5. Liao, A.P., Bai, Z.Z. and Lei, Y. (2005) Best Approximation Solution of Matrix Equation AXC+BYD=E. SIAM Journal on Matrix Analysis and Applications, 22, 675-688.
http://dx.doi.org/10.1137/040615791 - 6. Xu, G., Wei, M. and Zheng, D. (1998) On the Solutions of Matrix Equation AXB+CYD=F. Linear Algebra and Its Applications, 279, 93-109.
http://dx.doi.org/10.1016/S0024-3795(97)10099-4 - 7. Chang, X.W. and Wang, J.S. (1993) The Symmetric Solution of the Matrix Equations AX+YA=C, AXAT+BYBT=C and (ATXA,BTXB)=(C,D). Linear Algebra and Its Applications, 179, 171-189.
http://dx.doi.org/10.1016/0024-3795(93)90328-L - 8. Zietak, K. (1984) The lp-Solution of the Linear Matrix Equation AX+YB=C. Computing, 32, 153-162.
http://dx.doi.org/10.1007/BF02253689 - 9. Zietak, K. (1985) The Chebyshev Solution of the Linear Matrix Equation AX+YB=C. Numerische Mathematik, 46, 455-478.
http://dx.doi.org/10.1007/BF01389497 - 10. Peng, Z.Y. (2004) The Nearest Bisymmetric Solutions of Linear Matrix Equations. Journal of Computational Mathematics, 22, 873-880.
- 11. Ding, F., Liu, P.X. and Ding, J. (2008) Iterative Solutions of the Generalized Sylvester Matrix Equations by Using the Hierarchical Identification Principle. Applied Mathematics and Computation, 197, 41-50.
http://dx.doi.org/10.1016/j.amc.2007.07.040 - 12. Peng, Z.Y. and Peng, Y.X. (2006) An Efficient Iterative Method for Solving the Matrix Equation AXB+CYD=E. Numerical Linear Algebra with Applications, 13, 473-485.
http://dx.doi.org/10.1002/nla.470 - 13. Peng, Z.Y. (2005) A Iterative Method for the Least Squares Symmetric Solution of the Linear Matrix Equation AXB=C. Applied Mathematics and Computation, 170, 711-723.
http://dx.doi.org/10.1016/j.amc.2004.12.032 - 14. Peng, Z.H., Hu, X.Y. and Zhang, L. (2007) The Bisymmetric Solutions of the Matrix Equation A1X1B1+A2X2B2+…+AiXiBi=C and Its Optimal Approximation. Linear Algebra and Its Applications, 426, 583-595.
http://dx.doi.org/10.1016/j.laa.2007.05.034 - 15. Lei, Y. and Liao, A.P. (2007) A Minimal Residual Algorithm for the Inconsistent Matrix Equation AXB=C over Symmetric Matrices. Applied Mathematics and Computation, 188, 499-513.
http://dx.doi.org/10.1016/j.amc.2006.10.011 - 16. Zhou, F.Z., Hu, X.Y. and Zhang, L. (2003) The Solvability Conditions for the Inverse Eigenvalue Problems of Centro-Symmetric Matrices. Linear Algebra and Its Applications, 364, 147-160.
http://dx.doi.org/10.1016/S0024-3795(02)00550-5 - 17. Xie, D.X., Zhang, L. and Hu, X.Y. (2000) The Solvability Conditions for the Inverse Problem of Bisymmetric Nonnegative Definite Matrices. Journal of Computational Mathematics, 6, 597-608.
- 18. Wang, R.S. (2003) Function Analysis and Optimization Theory. Beijing University of Aeronautics and Astronautics Press, Beijing. (In Chinese)
NOTES

*Corresponding author.
上一篇:Jordan Γ*-Derivation on 下一篇:Matrices and Division by Zero
最新文章NEWS
- On Characterization of Poised Nodes for a Space of Bivariate Functions
- Least-Squares Solutions of Generalized Sylvester Equation with Xi Satisfies Different Linear Constra
- Matrices and Division by Zero z/0 = 0
- Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution
- Two Nonzero Component Lemma and Matrix Trigonometry
- Using Row Reduced Echelon Form in Balancing Chemical Equations
- Tight Monomials with t-Value ≤ 9 for Quantum Group of Type D4
- Minimum Covering Randić Energy of a Graph
推荐期刊Tui Jian
- Chinese Journal of Integrative Medicine
- Journal of Genetics and Genomics
- Journal of Bionic Engineering
- Pedosphere
- Chinese Journal of Structural Chemistry
- Nuclear Science and Techniques
- 《传媒》
- 《中学生报》教研周刊
热点文章HOT
- Using Row Reduced Echelon Form in Balancing Chemical Equations
- Minimum Covering Randić Energy of a Graph
- A Note on the Inclusion Sets for Tensors
- A General Hermitian Nonnegative-Definite Solution to the Matrix Equation AXB = C
- Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution
- Matrices and Division by Zero z/0 = 0
- On Characterization of Poised Nodes for a Space of Bivariate Functions
- Pseudo Laguerre Matrix Polynomials, Operational Identities and Quasi-Monomiality
