欢迎来到期刊吧-专注期刊发表！
关于我们联系我们发表流程付款方式医学sci转让留言板
您的位置： 首页 > 国外期刊 > Advances in Linear Algebra & Matrix Theory

Partial Ordering of Range Symmetric Matrices and M-Projectors with Respect to Minkowski Adjoint in M

Vol.06No.04(2016), Article ID:72565,14 pages
10.4236/alamt.2016.64013

D. Krishnaswamy, Mohd Saleem Lone

Department of Mathematics, Annamalai University, Chidambaram, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

Received: October 6, 2016; Accepted: December 3, 2016; Published: December 6, 2016

ABSTRACT

In this paper, we obtain some new characterizations of the range symmetric matrices in the Minkowski Space by using the Block representation of the matrices. These characterizations are used to establish some results on the partial ordering of the range symmetric matrices with respect to the Minkowski adjoint. Further, we establish some results regarding the partial ordering of m-projectors with respect to the Minkowski adjoint and manipulate them to characterize some sets of range symmetric elements in the Minkowski Space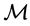. All the results obtained in this paper are an extension to the Minkowski space of those given by A. Hernandez, et al. in [The star partial order and the eigenprojection at 0 on EP matrices, Applied Mathematics and Computation, 218: 10669-10678, 2012].

Keywords:

Partial Order, Minkowski Adjoint, Minkowski Inverse, Range Symmetric, M-Projectors

1. Introduction and Preliminaries

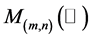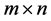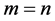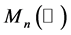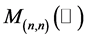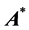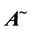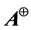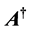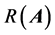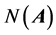Let us denote by the set of matrices and when we write for. The symbols, , , , and de- note the conjugate transpose, Minkowski adjoint, Minkowski inverse, Moore-Penrose inverse, range space and null space of a matrix 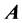respectively. 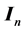denote the iden- tity matrix of order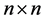. Further we denote by 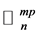the set of all m-projections. i.e.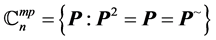. Also we use the convection according to which and. Where is the identity matrix of suitable order. r and s will denote the rank of the matrices and.

Indefinite inner product is a scalar product defined by

(1)

where denotes the conventional Hilbert Space inner product and is a Hermitian matrix. This Hermitian matrix is referred to as metric matrix. Min- kowski Space is an indefinite inner product space in which the metric matrix

is denoted by and is defined as satisfying and.

is called the Minkowski metric matrix. In case, then is called the Minkowski metric tensor and is defined as. For detailed study of indefinite linear algebra refer to [1] .

The minkowski inverse of a matrix, introduced by Meenakshi in [2] , is the unique solution to the following four matrix equations:

[MI-1]:.

[MI-2]:.

[MI-3]:.

[MI-4]:.

However unlike the Moore-Penrose inverse of a matrix, the Minkowski inverse of a matrix does not exist always. In [2] , Meenakshi showed that the Minkowski inverse of a matrix exists if and only if, where is called the Minkowski adjoint of the matrix and and are the Minkowski metric matrices of suitable order m and n. A matrix is said to be m-symmetric if and is said to be G-unitary if and only if . In [3] , Meenakshi introduced the concept of range symmetric matrices in Minkowski Space and developed the Minkowski inverse of the range symmetric matrices and some equivalent conditions for a matrix to be range symmetric. A matrix is said to be range symmetric if and only if. In [4] , the authors produced the necessary and sufficient conditions for the product of range symmetric matrices to be range symmetric and further showed that any block matrix in Minkowski space can be expressed as the product of range symmetric matrices. In [5] the authors studied the range symmetric matrices in relation with their Minkowski inverse and m-projectors. Summarizing the equivalent conditions for the definition of a range symmetric matrix form [3] [5] [6] the following equivalent con- ditions will be used in the forthcoming results:

[RS-1]: is range symmetric.

[RS-2]:.

[RS-3]:.

[RS-4]:.

[RS-5]: their exist a G-unitary matrix such that.

Partial orders on matrices has remained the topic of interest for many authors in the area of matrix theory and generalized inverse. Almost all authors who have worked on partial ordering of matrices have formulated the definition involving different kinds of generalized inverses and in particular the Moore-Penrose Inverse. Results involving partial orders on matrices in relation with their generalized inverse are scattered in the literature of the matrix theory and generalized inverses for instance see [7] - [19] . Partial ordering on matrices has a wide range of applications in different fields which include electrical networks, statistics, generalized inverses etc. see [20] [21] [22] [23] . Different kinds of partial orders on matrices have been studied which include Star partial ordering introduced by Drazin [24] , minus partial order introduced by Hartwig [25] , Sharp partial order introduced by Mitra [19] , followed by left star ordering and right star ordering. In [26] , Punithavalli introduced the partial ordering on matrices in Minkowski space w.r.t the Minkowski adjoint. She studied the partial ordering, left partial ordering and right partial ordering w.r.t the Minkowski adjoint on Range symmetric matrices. She also established some equivalent conditions for the reverse order law to hold in relation to the partial ordering w.r.t Minkowski adjoint. Form ( [26] , page 79), we have for any two matrices, is said to be below under the partial order w.r.t Minkowski adjoint, denoted by, if one of the following equivalent condition is satisfied:

[PO-1]: and.

[PO-2]: and.

[PO-3]: and.

In any of the above cases we say is predecessor of or is successor of. We will use the notation to denote the set of all the matrices of index k.

In this paper we obtain some characterizations of range symmetric matrices and utilize them to study the partial ordering of range symmetric matrices w.r.t the Min- kowski adjoint in Minkowski space and hence different characterizations of partial orders on range symmetric matrices are obtained. Finally we study the partial ordering on m-Projectors w.r.t the Minkowski adjoint. All the results obtained in this paper are an extension of those given in [27] to the Minkowski space.

2. Properties of Range Symmetric Matrices

In this section we develop some properties of Range Symmetric matrices by utilizing the representation obtained in corollary in [5] . Let be non-zero range symmetric matrices of rank and respectively. Then and, accord- ing to the above mentioned result, can be written as

(2)

and

(3)

where and are G-unitary and and are invertible matrices of order

Theorem 1 Let be such that is range symmetric. Then the fol- lowing statements are equivalent:

1.

2. If is given by (2), then there exists and such that with.

Proof. We consider the decomposition of the matrix, according to the size of blocks of, as:

.

From the statement (i) of the theorem, we get

.

This gives, and and hence the result follows.

If both the matrices and are range symmetric, then we have the following result for the commutativity.

Theorem 2 Let be range symmetric matrices. If Then the following statements are equivalent:

1..

2..

3..

Proof. (i)⇔(ii) Consider the representations of and given by (2) and (3) res- pectively. With given, we have

(4)

Also

Therefore

(5)

From Equations (4) and (5) we have

(6)

Pre multiplying and post multiplying (6) by and respectively and sub- stituting the matrix representation of and we get

From this equality, on using the fact that and are nonsingular, we have, , and and hence the equivalence follows.

(i)⇔(iii) From, using the fact that is G-unitary, we have and hence. Substituting the re- presentations of and in the block representation of given by (3) we have

Furthermore, doing some algebra we have,

Therefore the equality, on using the fact that, and are nonsingular, gives

Hence the equivalence follows.

Theorem 3 Let be such that exists. Then the following state- ments are equivalent:

1. is range symmetric.

2..

3..

Proof. (i)⇔(ii) Since and are m-symmetric idempotents, in fact m- projectors, on using [RS-3], we have is range symmetric if and only if . Also from [MI-1] and [MI-2] we have and . Therefore. Hence the equivalence follows.

(i)⇔(iii) Similarly and are idempotents such that

and. Again using [RS-3], the result fol- lows.

Theorem 4 Let be a non zero matrix. Then the following statements are equivalent:

1. is range symmetric.

2. There exists an invertible matrix and such that with.

3. There exists an invertible matrix and such that with

Proof. (i)⇔(ii) Using [RS-4], there exists an invertible matrix such that. We partition according to the blocks of such that

Now, gives, using the fact that is in- vertible and is G-unitary.

(i)⇔(iii) From statement (ii) of the Theorem 3 and [RS-4], we have, the equivalence follows on the same lines as above

Theorem 5 Let be a nonzero matrix. Then the following statements are equivalent:

1. is range symmetric.

2. There exists an invertible matrix and such that with.

3. There exists an invertible matrix and such that with.

Proof. The proof follows on the same lines as in the above theorem, using the fact that two matrices and are row equivalent if and only if and utilizing the statement (iii) of Theorem 3 and [RS-2].

3. Partial Ordering of Range Symmetric Matrices w.r.t Minkowski Adjoint

In this section some characterizations of predecessors of range symmetric matrices under the partial ordering w.r.t Minkowski adjoint. Using the equivalences of the defi- nition of Partial ordering w.r.t Minkowski adjoint that is [PO-1] and, [PO-2], it can

be easily verified that and are m-symmetric.

Theorem 6 Let such that is a nonzero range symmetric matrix. Then the following statements are equivalent:

1..

2. There exists such that

(7)

Proof. (i)⇔(ii) We consider the following block representation of according to the block size of as:

Then

and

Therefore the equality gives and and Also computing and and using the equality, we get and. Thus and i.e.,.

However if is range symmetric and, then need not be range sym- metric e.g. consider the matrices

Example 1

Remark 1 If both the matrices are range symmetric and, then using the statements [PO-1], [PO-2] and [RS-3], it can be easily observed that. Using the representations (3) and (7) of and respectively and Theorem 6.8.3. from [26] , we have another equivalent condition for the partial ordering of range symmetric matrices w.r.t minkowski adjoint given by and. Furthermore, is range symmetric, we have.

The next result gives some equivalent conditions for a matrix to be range symmetric when is range symmetric and is the successor of.

Theorem 7 Let such that is a nonzero range symmetric matrix and, where is given by (3) and is given by (7). Then the following statements are equivalent:

1. is range symmetric.

2..

3..

4..

5..

6. is range symmetric.

Proof. (i)⇔(ii) From remark 1, we have. Now using the facts that ; being invertible and is G-unitary and substituting the repre- sentations of and from (3) and (7) respectively in the above equality and doing some simple algebra leads to

(ii)⇔(iii) For,. Again using Remark 1 and substituting the respective representations of and, the equivalence follows.

(ii)⇔(iv) Using [PO-1] and substituting the representations of, and, the equivalence follows after some computation.

On the same lines the equivalences (ii)⇔(v) and (iii)⇔(vi) follow by using the Remark 1 and statements [PO-1] and [PO-2].

The next result similar to Theorem 6 holds if we consider to be range symmetric and decompose in terms of representation for

Theorem 8 Let such that is a nonzero range symmetric matrix. Then the following statements are equivalent:

1..

2. There exists such that

(8)

Proof. The proof follows on the same line as in Theorem 6

We again note that if and is range symmetric, then need not be range symmetric. Consider Example 1. In the following result we establish some equivalent conditions for when is range symmetric and.

Theorem 9 Let be given by (2) and (8) respectively such that is a nonzero range symmetric matrix and. Then the following statements are equivalent:

1. is range symmetric.

2. is range symmetric.

3..

4..

Proof. (i)⇔(ii) For, since is nonsingular and is G- unitary, direct verification shows that. Therefore and. being range sym- metric, by [RS-3] we have. This gives and the equi- valence follows.

(i)⇒(iii) Since and and are range symmetric, using the observation mentioned in Remark 1 i.e., , we have, the equivalence follows.

(iii)⇒(i) Since and is range symmetric, again by the same fact that and commute, using (iii) i.e., , we get is range symmetric.

(i)⇔(iv) From Remark 1, we have. This gives. Now using the fact that is range symmetric the equivalence follows.

In the above results we have used the commutativity of and and and. However if we assume the conditions given in the above theorem with an additional assumption that, then the conditions obtained by interchanging and are also equivalent.

Theorem 10 Let be range symmetric such that is a non zero matrix. Then the following statements are equivalent:

1..

2. There exists a G-unitary matrix, and such that and

Proof. (i)⇒(ii) Consider the decomposition of given by (3) i.e., . Since is range symmetric, therefore by Theorem 6, there exists such that with. Using Theorem 7, we have is range symmetric. We consider the following block representation of as, where is G-unitary and is invertible. Since , by Theorem 8, we can find such that. Thus is nonsingular when. Taking, we have , where is G-unitary.

Follows at once by direct verification.

4. Partial Ordering of M-Projectors

In this section we obtain some results on partial ordering of m-projectors w.r.t Minkowski adjoint. The following result from [5] , with two more obvious conditions, will be used extensively in the forthcoming results.

Lemma 1 Let be range symmetric, then

1..

2. is idempotent.

3..

4. if and only if is nonsingular.

5. then.

6..

7. is invertible then and if, then.

8. has index atmost one.

Lemma 2 Let. Then

1. If, then.

2..

3. is invertible.

4. If is nonzero singular matrix then and are incomparable under the partial ordering w.r.t Minkowski adjoint.

5., then.

6..

Proof. (i) Since. This gives .

(ii), then. Conversely if, and and hence.

(iii) From statement (ii) of Lemma 1 and the fact that, if, then and hence by point (iv) of Lemma 1 is invertible. Again by the same argument i.e, point (iv) of Lemma 1 converse holds.

(iv) It is obvious from (ii) and (iii).

(v) Follows at once by using point (i) of the Lemma 2 and point (vi) of Lemma 1.

(vi) The statement follows at once on using the fact that.

Lemma 3 Let. Then

1. If is range symmetric, then is m-symmetric and hence range symmetric

2. If is range symmetric, then so is

Proof. (i) The statement follows at once on using the [RS-3], [MI-3] and [MI-4].

(ii) If, the the result is trivial. Let such that, then by point (v) of Lemma 1 we have. Also using point (ii) of Lemma 1 we get i.e.,. Thus we have. Consider the block re- presentation of, where the partition is done according to the blocks of such that. Using [MI-1] and [MI-2], we get. Therefore. This shows that is nonsingular and the result follows.

Remark 2 Since is a m-projector [5] , we have. If we write

i.e., we take as a function of, then

. Thus. However

in general. Consider the decomposition, we have

i.e, , which is the fundamental represen- tation of a m-projector. Hence we conclude that if and only if is a m- projector.

We generalize the function by defining it as:

(9)

Thus we have the following equations

(10)

and hence if R = 0, we get

(11)

Let us consider some sets with following notations:

(12)

(13)

and

(14)

Theorem 11 Let and be the sets defined in (12), (13) and (14) respectively. Then, and.

Proof. The proof follows easily by utilizing Lemmas 1 and 3.

From the statement (i) of Lemma 3, it is obvious that. However the reverse inclusion does not hold in general. Consider the matrix. If possible suppose there exist a matrix such that, then by Lemma 3, we have, which is absurd, since but. There- fore.

Remark 3 Let, then by using Lemma 1. If , then by Remark 2, we have and if, then by Theorem 11, we have.

The next result provides a characterization of the set

Theorem 12 Let be range symmetric given by (2), then

Proof. Let. Then. Therefore for , we have such that i.e., and the result follows.

The next result shows that the function, when restricted to the set is mo- notonically decreasing w.r.t the partial ordering w.r.t Minkowski adjoint.

Theorem 13 Let, such that. Then

Proof. Let, such that. Since is range symmetric we have

and therefore

(15)

Also

(16)

Finally using (15) and (16) we get and. Hence.

However for the range symmetric matrices and, we have but. Thus we have the following result.

Theorem 14 Let, such that. Then.

Proof. The proof follows at once by using Theorem 13 and Remark 2.

Theorem 15 Let be range symmetric and be such that. Then.

Proof. Consider the decomposition of as given in (2). Then from Theorem 8 we get and hence. Thus if we assume , then from Theorem 6, we get with. There- fore. Hence Conversely if we assume that, then is range symmetric and finally from Theorem 13, the result follows.

Theorem 16 Let has the representation as given in point of Lemma 1 and. Then if and only if there exists such that

Proof. Assume that. Then from Theorem 13 we have . Let, where the blocks are partitioned according to the blocks of. Using the above mentioned equality we have, and and hence Also

. Taking, where the decomposition is done according to the blocks of. Then from the equation we get, , , and and therefore with. Clearly has index one. The converse is obvious.

Acknowledgements

The second author was supported by UGC-BSR through grant No. F25-1/2014-15(BSR)/ 7-254/2009(BSR) (20.01.2015). This support is greatly appreciated.

Cite this paper

Krishnaswamy, D. and Lone, M.S. (2016) Partial Ordering of Range Symmetric Matrices and M-Projectors with Respect to Minkowski Adjoint in Min- kowski Space. Advances in Linear Algebra & Matrix Theory, 6, 132-145. http://dx.doi.org/10.4236/alamt.2016.64013

References

  1. 1. Gohberg, I., Lancaster, P. and Rodman, L. (2005) Indefinite Linear Algebra and Applications. Birkhauser, Verlag, Basel, Boston, Berlin.

  2. 2. Meenakshi, A.R. (2000) Generalized Inverse of Matrices in Minkowski Space. Proceedings of National Seminar on Algebra and Its Applications, 1, 1-14.

  3. 3. Meenakshi, A.R. (2000) Range Symmetric Matrices in Minkowski Space. Bulletin of the Malaysian Mathematical Sciences Society, 23, 45-52.

  4. 4. Meenakshi, A.R. and Krishnaswamy, D. (2006) Product of Range Symmetric Block Matrices in Minkowski Space. Bulletin of the Malaysian Mathematical Sciences Society, 29, 59-68.

  5. 5. Lone, M.S. and Krishnaswamy, D. (2016) m-Projections Involving Minkowski Inverse and Range Symmetric Property in Minkowski Space. Journal of Linear and Topological Algebra.

  6. 6. Krishnaswamy, D. (2005) Contributions to the Study on Range Symmetric Matrices in Minkowski Space. Ph.D. Dissertation, Annamalai University, India.

  7. 7. Ben-Isreal, A. and Greville, T. (2003) Generalized Inverse: Theory and Applications. 2nd Edition, Springer Verlag, New York.

  8. 8. Campbell, S.L. and Meyer Jr., C.D. (1991) Generalized Inverse of Linear Transformations. 2nd Edition, Dover, New York.

  9. 9. Prasolov, V.V. (1994) Problems and Theorems in Linear Algebra. American Mathematical Society, Providence.

  10. 10. Meyer, C.D. (2000) Matrix Analysis and Applied Linear Algebra. SIAM, Philadelphia.
    https://doi.org/10.1137/1.9780898719512

  11. 11. Mitra, S.K., Bhimasankaram, P. and Malik, S.B. (2010) Matrix Partial Orders, Shorted Operators and Applications. World Scientific Publishing Company, Singapore.

  12. 12. Rao, C.R. and Mitra, S.K. (1971) Generalized Inverse of Matrices and Its Applications. John Wiley & Sons, New York.

  13. 13. Tosic, M. and Cvetkovic-Ilic, D.S. (2012) Invertibility of a Linear Combination of Two Matrices and Partial Orderings. Applied Mathematics and Computation, 218, 4651-4657.
    https://doi.org/10.1016/j.amc.2011.10.052

  14. 14. Malik, S.B. (2013) Some More Properties of Core Partial Order. Applied Mathematics and Computation, 221, 192-201.
    https://doi.org/10.1016/j.amc.2013.06.012

  15. 15. Malik, S.B., Ruedab, L. and Thome, N. (2014) Further Properties on the Core Partial Order and Other Matrix Partial Orders. Linear Multilinear Algebra, 62, 1629-1648.
    https://doi.org/10.1080/03081087.2013.839676

  16. 16. Baksalary, J.K. and Mitra, S.K. (1991) Left-Star and Right-Star Partial Orderings. Linear Algebra and Its Applications, 149, 73-89.
    https://doi.org/10.1016/0024-3795(91)90326-R

  17. 17. Deng, C.Y. and Wang, S.Q. (2012) On Some Characterizations of the Partial Orderings for Bounded Operators. Mathematical Inequalities & Applications, 15, 619-630.
    https://doi.org/10.7153/mia-15-54

  18. 18. Liu, F.X. and Yang, H. (2011) Some Results on the Partial Orderings of Block Matrices. Journal of Inequalities and Applications, 2011, 1-7.
    https://doi.org/10.1186/1029-242x-2011-54

  19. 19. Mitra, S.K. (1987) On Group Inverses and the Sharp Order. Linear Algebra and Its Applications, 92, 17-37.
    https://doi.org/10.1016/0024-3795(87)90248-5

  20. 20. Baksalary, J.K., Hauke, J. and Styan, G.P.H. (1994) On Some Distributional Properties of Quadratic Forms in Normal Variables and on Some Associated Matrix Partial Orderings. Multivariate Analysis and Its Applications, 24, 111-121.

  21. 21. Baksalary, J.K. and Puntanen, S. (1990) Characterizations of the Best Linear Unbiased Estimator in the General Gauss Markov Model with the Use of Matrix Partial Orderings. Linear Algebra and Its Applications, 127, 363-370.
    https://doi.org/10.1016/0024-3795(90)90349-H

  22. 22. Puntanen, S. and Styan, G.P.H. (2015) Best Linear Unbiased Estimation in Linear Models (Version 8). StatProb: The Encyclopedia Sponsored by Statistics and Probability Societies.

  23. 23. Stepniak, C. (1987) Ordering of Nonnegative Definite Matrices with Application to Comparison of Linear Models. Linear Algebra and Its Applications, 70, 67-71.
    https://doi.org/10.1016/0024-3795(85)90043-6

  24. 24. Drazin, M.P. (1978) Natural Structures on Semi Groups with Involution. Bulletin American Mathematical Society, 84, 139-141.
    https://doi.org/10.1090/S0002-9904-1978-14442-5

  25. 25. Hartwig, R.E. (1980) How to Partially Order Regular Elements? Japanese Journal of Mathematics, 25, 1-13.

  26. 26. Punithavalli, G. (2014) Contributions to the Study on Various Solutions of the Matrix Equation AXB=C in Minkowski Space M. PhD Dissertation, Annamalai University, Annamalai Nagar.

  27. 27. Hernnandez, A., Lattanzi, M., Thome, N. and Urquiza, F. (2012) The Star Partial Order and the Eigenprojection at 0 on EP Matrices. Applied Mathematics and Computation, 218, 10669-10678.
    https://doi.org/10.1016/j.amc.2012.04.034

上一篇:Jordan Γ*-Derivation on 下一篇:A QMR-Type Algorithm for Drazi

我要分享到：