Applications of Arithmetic Geometric Mean Inequality
Vol.07No.02(2017), Article ID:77048,8 pages
10.4236/alamt.2017.72004
Wasim Audeh
Department of Mathematics, University of Petra, Amman, Jordan

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 26, 2017; Accepted: June 18, 2017; Published: June 21, 2017
ABSTRACT
The well-known arithmetic-geometric mean inequality for singular values, due to Bhatia and Kittaneh, is one of the most important singular value inequalities for compact operators. The purpose of this study is to give new singular value inequalities for compact operators and prove that these inequalities are equivalent to arithmetic-geometric mean inequality, the way by which several future studies could be done.
Keywords:
Compact Operator, Inequality, Positive Operator, Singular Value

1. Fundamental Principles
Let 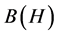 indicate the set of all bounded linear operators on a complex separable Hilbert space H, and let
indicate the set of all bounded linear operators on a complex separable Hilbert space H, and let  indicate the two-sided ideal of compact operators in
indicate the two-sided ideal of compact operators in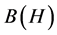 . If
. If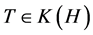 , the singular values of T, denoted by
, the singular values of T, denoted by 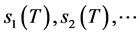 are the eigenvalues of the positive operator
are the eigenvalues of the positive operator 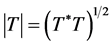 ordered as
ordered as  and repeated according to multiplicity. It is well known that
and repeated according to multiplicity. It is well known that 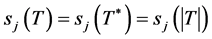 for
for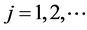 . It follows by Weyl’s monotonicity principle (see, e.g., [1] , p. 63 or [2] , p. 26) that if
. It follows by Weyl’s monotonicity principle (see, e.g., [1] , p. 63 or [2] , p. 26) that if
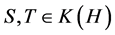 are positive and
are positive and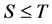 , then
, then 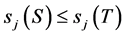 for
for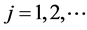 . Moreover, for
. Moreover, for 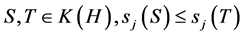 if and only if
if and only if
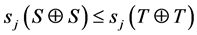 for
for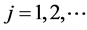 . Here, we use the direct sum notation
. Here, we use the direct sum notation
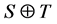 for the block-diagonal operator
for the block-diagonal operator 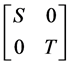 defined on
defined on . The sin- gular values of
. The sin- gular values of  and
and  are the same, and they consist of those of
are the same, and they consist of those of
S together with those of T.
Bhatia and Kittaneh have proved in [3] that if  such that
such that  is self-adjoint,
is self-adjoint,  , and
, and , then
, then
 (1.1)
(1.1)
for .
.
Audeh and Kittaneh in [4] prove inequality which is equivalent to inequality (1.1):
If  such that
such that , then
, then
 (1.2)
(1.2)
for .
.
The well-known arithmetic-geometric mean inequality for singular values, due to Bhatia and Kittaneh [5] , says that if , then
, then
 (1.3)
(1.3)
for . On the other hand, Zhan has proved in [6] that if
. On the other hand, Zhan has proved in [6] that if  are positive, then
are positive, then
 (1.4)
(1.4)
for . Moreover, Tao has proved in [7] that if
. Moreover, Tao has proved in [7] that if  such
such
that , then
, then
 (1.5)
(1.5)
for .
.
Audeh and Kittaneh have proved in [4] that:
If  such that
such that  is self-adjoint,
is self-adjoint,  , and
, and , then
, then
 (1.6)
(1.6)
for .
.
It has been pointed out in [4] that the four inequalities (1.3)-(1.6) are equi- valent.
Moreover, Tao in [7] uses inequality (1.3) to prove that if  and
and  are positive operators in
are positive operators in ,
, . Then
. Then
 (1.7)
(1.7)
for .
.
2. Introduction
In this study, we will present several new inequalities, and prove that they are equivalent to arithmetic-geometric mean inequality.
The following are the proved inequalities in this study:
Let  and
and  be operators in
be operators in  where
where ,
,  and
and  arbitrary operators. Then
arbitrary operators. Then
 (2.1)
(2.1)
for .
.
Let  and
and  be arbitrary operators in
be arbitrary operators in . Then we have
. Then we have
 (2.2)
(2.2)
for .
.
Let  be operators in
be operators in . Then
. Then
 (2.3)
(2.3)
for .
.
If  and
and  are operators in
are operators in . Then
. Then
 (2.4)
(2.4)
for .
.
Let  be positive operators in
be positive operators in  Then
Then
 (2.5)
(2.5)
for .
.
3. Main Results
Our first singular value inequality needs the following lemma.
Lemma 1: Let  be a positive operator in
be a positive operator in ,
,  be an arbitrary operator in
be an arbitrary operator in . Then we have
. Then we have
 (3.1)
(3.1)
Now we will prove the first Theorem which is equivalent to arithmetic- geometric mean inequality.
Theorem 3.1 Let  and
and  be operators in
be operators in  where
where ,
,  and
and  arbitrary operators. Then
arbitrary operators. Then

for .
.
Proof. Let  (because
(because  by assumption), and let
by assumption), and let
 . Then we have
. Then we have

From (1.5) we have

for .
.
Now we will prove that Theorem (3.1) is equivalent to arithmetic-geometric mean inequality.
Theorem 3.2 The following statements are equivalent:
1) Let , then
, then

for .
.
2) Let  and
and  be operators in
be operators in  where
where ,
,  and
and  arbitrary operators. Then
arbitrary operators. Then

for .
.
Proof. 1) ® 2) Let 
Now apply arithmetic-geometric mean inequality to get

for . But
. But

The above steps implies that
 for
for .
.
2) ® 1) The matrix  can be factorized as
can be factorized as
 , but it is well known that
, but it is well known that
 for
for . So
. So

for , from (2) we have
, from (2) we have
 (3.2)
(3.2)
for . Now let
. Now let  in Inequality (3.2) we get
in Inequality (3.2) we get
 (3.3)
(3.3)
for , which is the arithmetic-geometric mean inequality.
, which is the arithmetic-geometric mean inequality.
The following lemma which was proved by Bhatia [1] is essential to prove the next theorem.
Lemma 2 Let  be arbitrary operator in
be arbitrary operator in . Then
. Then
 (3.4)
(3.4)
Now we will prove the following theorem which is more general than Theo- rem (3.1) and equivalent to arithmetic-geometric mean inequality.
Theorem 3.3 Let  and
and  be arbitrary operators in
be arbitrary operators in . Then we have
. Then we have

for .
.
Proof. Applying Lemma (2) gives  for an arbitrary ope- rator
for an arbitrary ope- rator . Let
. Let  by using Inequality (3.1) we have
by using Inequality (3.1) we have
 Hence using Inequality (1.5) gives
Hence using Inequality (1.5) gives
 .
.
Remark 1 Theorem (3.3) is generalization of Theorem (3.1) because here X is arbitrary operator but there A should be positive operator.
Remark 2 Inequality (2.2) is equivalent to arithmetic-geometric mean inequality. We can prove this equivalent by similar steps used to prove Theorem (3.2).
The following theorem is a generalization of Theorem (3.1) and Theorem (3.3).
Theorem 3.4 Let  and
and  be arbitrary operators in
be arbitrary operators in . Then we have
. Then we have

for .
.
Proof. Let  Then
Then
 Hence
Hence

use Inequality (1.5) to get the required result.
Remark 3 Replace B, D by 0 in Inequality (2.4) will gives Inequality (2.1).
Remark 4 Replace A, C by 0 in Inequality (2.4) will also gives Inequality (2.1).
Now we will use Inequality (1.3) to prove the following theorem, then we will show that they are equivalent.
Theorem 3.5 Let  be operators in
be operators in . Then
. Then

for .
.
Proof. Let  Then
Then  and
and
 Now use Inequality (1.3) we get
Now use Inequality (1.3) we get

for .
.
Now we will prove that Inequality (2.3) is equivalent to Inequality (1.3).
Theorem 3.6 The following statements are equivalent:
1) Let . Then
. Then

for .
.
2) Let  be operators in
be operators in . Then
. Then

for .
.
Proof. 1) ® 2) It is the proof of Theorem (3.5).
2) ® 1) By replacing  and
and  in Inequality (2.3), we
in Inequality (2.3), we
get  From this we reach to
From this we reach to
 which implies that
which implies that  for
for .
.
In the rest of this paper, we will prove new inequality which is equivalent to Inequality (1.7).
Theorem 3.7 Let  be positive operators in
be positive operators in , n is an even integer,
, n is an even integer, . Then
. Then
 (3.5)
(3.5)
for .
.
Proof. Let  Then we have
Then we have

and  Now apply
Now apply
Inequality (1.7) we get the result.
We will prove that Inequality (1.7) is equivalent to Inequality (3.5).
Theorem 3.8 The following statements are equivalent:
1) Let  and
and  be positive operators in
be positive operators in ,
, . Then
. Then

for .
.
2) Let  be positive operators in
be positive operators in , n is even integer,
, n is even integer, . Then
. Then

for .
.
Proof. 1) ® 2) This implication follows from the proof of Theorem 3.7.
2) ® 1) Let  in Inequality (3.5) to get
in Inequality (3.5) to get

for . But
. But  and
and  for
for
 .
.
If and only if , this gives
, this gives

for , replace
, replace  by
by ,
,  by
by  in this inequality we will get
in this inequality we will get

for .
.
4. Conclusion
Since this study has been completed, we can conclude that several singular value inequalities for compact operators are equivalent to arithmetic-geometric mean inequality, which in turns have many crucial applications in operator theory, and from this point we advise interested authors to join these results with results in other studies to make connection between several branches in operator theory.
Acknowledgements
The author is grateful to the University of Petra for its Support. The Author is grateful to the referee for his comments and suggestions.
Cite this paper
Audeh, W. (2017) Applications of Arithmetic Geometric Mean Inequality. Advances in Linear Algebra & Matrix Theory, 7, 29-36. https://doi.org/10.4236/alamt.2017.72004
References
- 1. Bhatia, R. (1997) Matrix Analysis, GTM169. Springer-Verlag, New York.
https://doi.org/10.1007/978-1-4612-0653-8 - 2. Gohberg, I.C. and Krein, M.G. (1969) Introduction to the Theory of Linear Nonselfadjoint Operators. American Mathematical Society, Providence.
- 3. Bhatia, R. and Kittaneh, F. (2008) The Matrix Arithmetic-Geometric Mean Inequality Revisited. Linear Algebra and Its Applications, 428, 2177-2191.
https://doi.org/10.1016/j.laa.2007.11.030 - 4. Audeh, W. and Kittaneh, F. (2012) Singular Value Inequalities for Compact Operators. Linear Algebra and Its Applications, 437, 2516-2522.
https://doi.org/10.1016/j.laa.2012.06.032 - 5. Bhatia, R. and Kittaneh, F. (1990) On the Singular Values of a Product of Operators. SIAM Journal on Matrix Analysis and Applications, 11, 272-277.
https://doi.org/10.1137/0611018 - 6. Zhan, X. (2000) Singular Values of Differences of Positive Semidefinite Matrices. SIAM Journal on Matrix Analysis and Applications, 22, 819-823.
https://doi.org/10.1137/S0895479800369840 - 7. Tao, Y. (2006) More Results on Singular Value Inequalities of Matrices. Linear Algebra and Its Applications, 416, 724-729.
https://doi.org/10.1016/j.laa.2005.12.017
上一篇:Jordan Γ*-Derivation on 下一篇:Two Nonzero Component Lemma an
最新文章NEWS
- On Characterization of Poised Nodes for a Space of Bivariate Functions
- Least-Squares Solutions of Generalized Sylvester Equation with Xi Satisfies Different Linear Constra
- Matrices and Division by Zero z/0 = 0
- Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution
- Two Nonzero Component Lemma and Matrix Trigonometry
- Using Row Reduced Echelon Form in Balancing Chemical Equations
- Tight Monomials with t-Value ≤ 9 for Quantum Group of Type D4
- Minimum Covering Randić Energy of a Graph
推荐期刊Tui Jian
- Chinese Journal of Integrative Medicine
- Journal of Genetics and Genomics
- Journal of Bionic Engineering
- Pedosphere
- Chinese Journal of Structural Chemistry
- Nuclear Science and Techniques
- 《传媒》
- 《哈尔滨师范大学自然科学学报》
热点文章HOT
- Using Row Reduced Echelon Form in Balancing Chemical Equations
- Minimum Covering Randić Energy of a Graph
- A Note on the Inclusion Sets for Tensors
- A General Hermitian Nonnegative-Definite Solution to the Matrix Equation AXB = C
- Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution
- Matrices and Division by Zero z/0 = 0
- On Characterization of Poised Nodes for a Space of Bivariate Functions
- Two Nonzero Component Lemma and Matrix Trigonometry
