ABSTRACT

We study the relations between several classes of matrices with variants of the diagonal dominance property, and identify those classes which form pairs of incomparable classes. For an incomparable pair 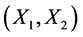of classes of matrices with variants of the diagonal dominance property, we also study the problem of providing sufficient conditions for the matrices in 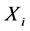to be in with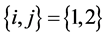. The article is a continuation of a series of articles on the topic and related topics by the author; see [1] [2] [3] [4] .

Keywords:

Doubly Diagonally Dominant, Generalized Diagonally Dominant, Separation Induced Diagonally Dominant, Row-Column Diagonally Dominant with Index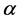

1. Introduction and Notation

The theory of matrices with variants of the diagonal dominance property has attracted the attention of researchers in matrix analysis and its applications. Desplanques [5] established the invertibility of every strictly diagonally dominant complex matrix; see Definition 2.1. (Lévy [6] established the result earlier for real matrices). The pioneering work of Lévy and Desplanques motivated researchers to study matrices with variants of the diagonal dominance property. For more results on the subject; see, for example, [1] and [3] - [25] . As usual, we denote the algebra of all matrices over the field of complex numbers by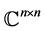. For every 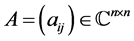and every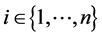, we define the row sum 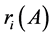and column sum 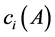by

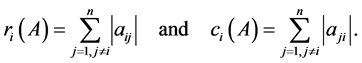(1.1)

In (1.1), it is understood that if A is a 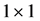matrix.

The objectives of this paper are to investigate the following two problems:

1) Identify among several classes of matrices with variants of the diagonal dominance property those which form pairs of incomparable classes. If 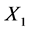and are subclasses of, we say that is a pair of incomparable classes if and.

2) If is a pair of incomparable classes of matrices in with variants of the diagonal dominance property, provide sufficient conditions for matrices in to be in, where. We investigate this problem for most pairs of incomparable classes identified in 1).

The set of positive integers is denoted by, and for every, we denote the set by. The empty set is denoted by. We denote the cardinality of a nonempty finite set S by. The set of all complex matrices is denoted by. The set is simply written as. If and is the entry of x in the ith row, , we write x as. We denote by 0 the zero matrix, and when there is a need to emphasize its size, we will use the symbol to denote the zero matrix in. The multiplicative group of invertible matrices is denoted by, and its identity is written as. Let. The entry of A is sometimes written as. The transpose of A is denoted by. If () for all and, we write (). The matrix is the matrix in defined by for all and. If is diagonal and is the ith diagonal entry of, , we denote by. If, the diagonal matrix is denoted by.

The set of eigenvalues of is denoted by, and the spectral radius of A is written as. So,. Similar matrices in have the same eigenvalues. Among similar matrices, those which are similar through diagonal matrices, are of particular interest. If

, we say that A is diagonally similar to B if there exists a diagonal matrix such that. The set of all matrices, which are diagonally similar to, is denoted by. If, we define the diagonal similarity orbit of by

(1.2)

Submatrices play a role in the development of the topics studied in the paper. Let, , and let S and T be nonempty subsets of. The submatrix of A that lies in the rows and columns of A indexed by S and T, respectively, is denoted by. If, we write simply as; see p. 17 of [26] . For every nonempty subset S of and each, it is instructive to evaluate the -norm of the off-diagonal entries among the ith row (column), which belong to the columns (rows) of A defined by the set S. Formally, we define and by

(1.3)

It is clear that and. The sums in (1.3) are used in association with the notion of separation of.

Definition 1.1 Let. If S is a nonempty proper subset of, we call the pair a separation of.

Remark 1.1 Let,. Let S be a subset of with

. If, where, then,

and for all.

The paper is organized as follows. In Section 2, we list the classes of matrices with variants of the diagonal dominance property, which we consider in the paper. Section 3 outlines some of the preliminary facts about the classes defined in Section 2. The section provides a motivation for the results in the remaining sections of the paper. In Section 4, we study in depth the relation between doubly diagonally dominant matrices and separation-induced doubly diagonally dominant matrices. We analyze in Section 5 the relation between the class of generalized diagonally dominant matrices and the class of separation-induced doubly diagonally dominant matrices. We also show that the former class forms with the class of doubly diagonally dominant matrices a pair of incomparable classes. In Section 6, we study the relations between the row-column diagonally dominant matrices with index and the other classes we considered in Section 2.

2. Matrices with Variants of the Diagonal Dominance Property

We outline in this section the classes of matrices we consider in the rest of the paper. Irreducible matrices play an important role in the development of the theory. A matrix is called irreducible if it not reducible. A matrix is called reducible if either and; or and B is similar by way of permutation to a strictly upper triangular block matrix; see Definition 6.2.21 in [26] . We denote the set of all irreducible matrices in by.

Definition 2.1 Let. Define the sets and by

(2.1)

1) The matrix A is called diagonally dominant if for all. If, we say that A is strictly diagonally dominant. We call A irreducibly diagonally dominant if and A is both diagonally dominant and irreducible. We say that A is generalized diagonally dominant if there exists a nonsingular diagonal matrix such that is diagonally dominant. We call A strictly generalized diagonally dominant (also known as nonsingular H-matrix; see [11] ) if there exists a nonsingular diagonal matrix such that. If there exists a nonsingular diagonal matrix such that is irreducibly diagonally dominant, we say that A is irreducibly generalized diagonally dominant.

In the following items, we assume.

2) We call A doubly diagonally dominant if

(2.2)

We say that A is strictly doubly diagonally dominant if the inequalities in (2.2) are all strict. If A is doubly diagonally dominant, irreducible and at least one of inequalities (2.2) is strict, we call A irreducibly doubly diagonally dominant.

3) Let be a separation of. We say that A is separation- induced doubly diagonally dominant if

(2.3)

for all and. A is called separation-induced strictly doubly diagonally dominant if is nonempty and the inequalities of (2.3) are strict for all and. We say that A is separation-induced irreducibly doubly diagonally dominant if A is irreducible, is nonempty, A is doubly diagonally dominant with respect to the separation and there exist and such that

(2.4)

4) Let. We call A row-column diagonally dominant with index if

(2.5)

If all the inequalities in (2.5) are strict, we say that A is strictly row-column diagonally dominant with index A is called irreducibly row-column diagonally dominant with index if A is irreducible, row-column diagonally dominant with index and there exists such that

(2.6)

Let To simplify the terminology, we introduce the following abbreviated notations:

(2.7)

(2.8)

In the following terminology, we assume:

(2.9)

If is a separation of, we introduce the notation

(2.10)

If, then

(2.11)

3. Preliminaries

Some of the important facts linking the classes introduced in Definition 2.1 are reviewed in this section. The information provide motivations for the results established in the subsequent sections.

Remark 3.1 Let. Then

1), and

.

In items (2)-(6), we assume:

2), and

.

3).

4) If is a separation of, then

i), and similar equalities hold for

and.

ii).

iii).

iv) If, then if and only if A is irreducible, and there exist and such that (2.4) holds and

(3.1)

v) and.

5), and

.

6) If, then

i).

ii).

iii).

iv).

v).

7) Let. The classes, and

depend on the separation of. For example, the irreducible matrix A defined by

satisfies but. Then from (ii) of item (4), we deduce that and, and from A being irreducible and (iii) of item (4), we see that

and.

The following fact is less obvious than the inclusions in (v) of item (4) of Remark 3.1.

Lemma 3.1 Let, and let be a separation of. Then.

Proof. Let. It follows from and (v) of item (4) of Remark 3.1 that. Then from and, we deduce that in order to show that, it remains to show the existence of and such that (2.4) is satisfied. From and being a separation of, there exists such that. Assume that. The other case is proven similarly. From and being a separation of, there exists such that. Thus from, , we get

Hence, with taking and, we obtain (2.4).

Using (1.2), the following lemma provides characterizations of the classes, and. The lemma somehow justifies the use of the word “generalized” in the titles for the 3 classes. We omit the proof.

Lemma 3.2 Let. Then, and.

Additional facts about the classes in Definition 2.1 are outlined in the following lemma.

Lemma 3.3 Let. Then:

1) and, and the two inclusions are proper.

2).

3) and for all.

4).

5).

6).

7) If is a separation of, then

(3.2)

and

(3.3)

8).

9) If, then

(3.4)

Remark 3.2 We make the following observations in regard to Lemma 3.3.

1) In item (1), the inclusion was established by Taussky ( [23] , Theorem II).

2) The inclusion of item (2) is proper; it was first proved by Ostrowski [19] .

3) If, the fact in item 3) was illustrated through examples in [21] and [25] .

4) Items (5) and (6) follow through a careful reading of the proof of Pro-

position 1 of [18] . If then. If

, then, where is the unique integer in satisfying (see (2.1)). If then

. If, then

, where m is the unique integer in satisfying.

5) In contrast to items (5) and (6), we observe that

For example, let. Then, but

. Note that for the separation of

, we have:

So,

Also, for the separation of, we have

. For the separation of

, the strict inequality (2.4) is not satisfied, since

for.

6) Gao and Wang ( [12] , Theorem 1) established (3.2). For every integer, the inclusion is proper. We consider the following two cases:

Case 1:. Define the matrix by

(3.5)

Then, with

(3.6)

we have. Thus. However, it can be shown that for every separation of, there exists a pair such that

Hence the matrix defined by (3.5) satisfies for any separation of.

Case 2:. Define by

(3.7)

where is the matrix defined by (3.5). It then follows from (3.5), (3.6) and case 1 that the diagonal matrix satisfies. Thus. Let be a separation of. From (3.5) and (3.7), it is clear that

and

So, to complete the proof that, it remains to consider the case:

It then follows that is a separation of. Hence from (3.7), we deduce that

for all. Then from case 1 and the fact that is a separation of, we see that there exist and such that

The integer 5 is the smallest integer we were able to find with which the inclusion of (3.2) is proper.

7) Item (8) follows from item (6) and (3.2).

8) Let. In contrast to the inclusion in item (8), we observe that

(3.8)

For example, let be defined by and for all. Then. It can be shown that

. We will use Theorems 4.1 and 5.2 to show that

for all; see Remark 5.2.

9) Theorem 2 of [12] establishes (3.3) through the two set inclusions. The second inclusion readily follows. In the proof of, it is assumed that and the separation of satisfy the additional condition:

(3.9)

In general, matrices in need not to satisfy (3.9); for example,

is in, but and

. It is possible to establish (3.3) without making the assumption (3.9) by slightly modifying the proof of Theorem 2 of [12] . However, we will use Theorem 5.2 to prove the first inclusion of (3.3); see Corollary 5.3.

10) In (3.4), Ostrowski [20] established the inclusion, and Hadjidimos ( [15] , Theorem 2.1) proved the inclusion

. Item (4) of Theorem 6.6 provides a simple different proof of Hadjidimos’s result.

Remark 3.3 1) In light of the facts given in items (5) and (6) of Lemma 3.3, we will analyze in more depth in Section 4 the relation between

and

.

2) We will show in Theorem 5.1 that the relation between and is in contrast to the relation between and (given by (3.2)).

To simplify the set up of some statements in Sections 4 and 6, we introduce Definition 3.1.

Definition 3.1 Let, and let be a nonempty subclass of. We say that is invariant under the permutation similarity transformation if for every permutation matrix and every, we have.

Remark 3.4 Let, and let be a separation of with.

1) The classes, , , , ,

and are all invariant under the permutation similarity transformation.

2) There exists a permutation matrix such that the linear transfor- mation defined by is an isomorphism from onto.

Similar observations could be stated for the pairs:

4. Matrices with the Doubly Diagonal Dominance Property vs. Matrices with the Separation-Induced Doubly Diagonal Dominance Property

We denote the Cartesian product of two nonempty sets X and Y by.

Theorem 4.1 Let, and let be a separation of. Then the elements of the set

are pairs of incomparable classes.

Proof. It follows from Remark 3.4 that it suffices to consider the case:

, where. Also, from Remark 3.1 (item (3), and (iii) of item (4)), we see that it suffices to show the existence of such that

(4.1)

and

(4.2)

We consider the following two cases:

Case 1:. Assume without loss of generality that. Define as follows:

(4.3)

Define by

(4.4)

Then A and B defined by (4.3) and (4.4) satisfy (4.1) and (4.2), respectively, in this case.

Case 2:. Define as follows:

(4.5)

Define by

and

(4.6)

Then A and B defined by (4.5) and (4.6) satisfy (4.1) and (4.2), respectively, in this case.

The following corollary is a direct consequence of items (5) and (6) of Lemma 3.3, and Theorem 4.1. The exclusion of in the corollary is by virtue of item (5) of Remark 3.1.

Corollary 4.1 Let. Then the inclusions

and

are proper.

Remark 4.1 1) It follows from (v) of item (4) of Remark 3.1 that in order to establish sufficient conditions for matrices in () to be in

(), it suffices to provide such conditions for matrices in the smaller classes (). Also, from Lemma 3.1 and item (4) of Lemma 3.3, we see that in order to present sufficient conditions for matrices in to be in, it suffices to provide such conditions for matrices in the smaller class. This provides the basis for the set-ups of Theorems 4.2-4.4.

2) Let, and let, and

. Then there exist such that (see (2.1)), and. Suppose that

is a separation of. Then

(4.7)

(4.8)

and

(4.9)

If and, then from we obtain

, but this contradicts that. The “not both” phrase in (4.7) follows from and. If and

, then from we get, but this con- tradicts that and are disjoint. The “not both” phrase in (4.8) follows from and. The facts in (4.9) are proved similarly to the ones in (4.8). We will use (4.7), (4.8) and (4.9) in Theorems 4.2, 4.3 and 4.4, respectively.

Theorem 4.2 Let, , and let be the integer such that. Suppose that is a separation of such that. In addition, assume that A satisfies one of the following two conditions:

Condition (1):.

Condition (2): for all.

Then.

Proof. Let. Then from, we get

(4.10)

and

(4.11)

where in (4.11), the first inequality follows from and the second inequality follows from. From (4.11), we see that if A satisfies either condition (1) or condition (2) then

. (Note that if A satisfies condition

(2) then, from and, we get for all.) Then from (4.10) and the fact that was chosen arbitrarily, the result follows.

Theorem 4.3 Let, , and let be the integer such that. Suppose that is a separation of such that. In addition, assume that. Then

.

Proof. Let. Then from, we deduce that

and, from and, we get

This proves.

Theorem 4.4 Let,. Let be the integer such that. Suppose that is a separation of such that. In addition, assume that A satisfies the following two conditions:

Condition (1):.

Condition (2): If then there exists such that

(4.12)

Then.

Proof. It follows from that,

and. From and (see item (2) of Remark 4.1), we deduce that. Then from, condition (1) and Theorem 4.2, we infer that

. So, it remains to show that there exist and such that (2.4) is satisfied. It follows from and

that

(4.13)

If, then, with the choice of any and any, we see from (4.13) that (2.4) is satisfied. Thus it remains to consider the case. In this case, we deduce from condition (2) that there exists such that (4.12) is satisfied. Hence from (see condition (1)), and, we get

Then (2.4) is satisfied with and.

Theorem 4.5 provides sufficient conditions for matrices in the classes

and to be in and, respec- tively. We prove item (2) of the theorem. Item (1) is proven similarly.

Theorem 4.5 Let be a separation of, , and let

be such that the following two conditions are satisfied:

Condition (1): for all with, and

for all with.

Condition (2): for all and for all.

Then

1) If then.

2) If then.

Proof. Assume that. Then

for all and, and there exist and such that (2.4) is satisfied. Thus from condition (2), we deduce that for all and, and. Hence from condition (1) and, we see that.

Remark 4.2 1) In item (2) of Theorem 4.5, the condition was not used to drive the result.

2) If is a separation of, , and, sufficient conditions for A to be in could be set by replacing the inequalities in condition (1) of Theorem 4.5 by strict inequalities and keeping condition (2) of the theorem as it is.

5. The Class vs. the Classes and

The first main result of this section is Theorem 5.1. In item (2) of the theorem, 5 is the smallest integer we were able to find, which satisfies the result. We denote the set of all separations of by.

Theorem 5.1 Let. Then

1) If is a separation of, then.

2) If, then, and for every separa-

tion of, the pair is a pair of incompar- able classes.

Proof. 1) Let be a separation of. Choose and, and define by and for all

. Then.

2) Let. We construct such that for any separation of. The idea is to perturb the matrix defined in item (6) of Remark 3.2. Consider the following two cases:

Case 1:. Define by

(5.1)

Then, with as defined by (3.6), we have. Table 1 illustrates that for any separation of.

Case 2:. Define by

(5.2)

where is defined by (5.1). Thus, with and given by (3.6), we deduce from (5.1) that. Hence. Let be a separation of. Assume first that either or.

Assume without loss of generality that. Choose. Then from, (5.1) and (5.2), we get

So, it remains to consider the case:

(5.3)

Since is a separation of and, we infer from (5.3) that is a separation of. Thus from (5.2), we see that

for all. Hence from case 1, we deduce there exist and

such that

As was chosen arbitrarily, we infer that

. For every separation of, the in-

comparability of the pair follows from the first part and item (1).

The following theorem provides sufficient conditions for matrices in

to be in.

Theorem 5.2 Let, and let be a separation of. Suppose that. In addition, assume that A satisfies the following two conditions:

Condition (1): There exists such that.

Condition (2): The sets and

are nonempty.

Then

1) We have

(5.4)

and

(5.5)

2) We have

(5.6)

and for every satisfying

(5.7)

the diagonal matrix defined by

(5.8)

is nonsingular and satisfies. In particular,.

3) If there exist and such that (2.4) is satisfied, then either

or, where is the nonsingular dia-

gonal matrix defined by (5.7) and (5.8).

Proof. 1) It follows from and condition (1) that the second inequality of (5.4) holds. Then from condition (2) and, we deduce that there exists such that, and that the first inequality of (5.4) holds as well. Now, let and. It then follows from and the definitions of and that

. Thus from (5.4), we get and

, and from the definition of, we obtain

. This completes the proof of (5.5).

2) It follows from, condition (2) and (5.5) that (5.6) holds. Let be a real satisfying (5.7), and define the diagonal matrix by (5.8). Hence from (in (5.6)) and (in (5.7)), we infer that is a diagonal matrix with positive diagonal entries. Also, from (5.8) and, it is clear that

(5.9)

for all and, and

(5.10)

for all. From the first strict inequality of (5.5), the definition of (in (5.6)) and (in (5.7)), we get for all. Then from the first equality of (5.9), and (5.10), we see that

(5.11)

for all. Since, we deduce from the definition of (in (5.6)) and (in (5.7)) that for all. Thus from the second equality of (5.9), and (5.10), we infer that

(5.12)

for all. Since and for all, we see from the first inequality of (5.4), (5.9) and (5.10) that

(5.13)

for all. Since for all, we deduce from the second inequality of (5.4), (5.9) and (5.10) that for all. Hence from (5.11)-(5.13), we infer that. Then from being a nonsingular diagonal matrix, we see that.

3) Assume that there exist and such that (2.4) is satisfied. We consider the following two cases:

Case 1: and. In this case, we have. Thus from (2.4), (5.6) and (5.7), we deduce that

Hence from, (5.9) and (5.10), the result follows.

Case 2: Either or. In this case, we have

(5.14)

Then from (2.4) and (5.4), we infer that and

. Thus from, (5.10) and (5.14), we see that either

or. Hence from (5.9), the result follows.

Corollary 5.1 Let. Then

1) For each separation of, we have

.

2).

Proof. 1) Let be a separation of, and let

be such that. We show that A satisfies conditions (1) and (2) of Theorem 5.2. It follows from Remark 1.1 and that condition (1) of Theorem 5.2 is satisfied. Also, from A being irreducible, we deduce that condition (2) of Theorem 5.2 is satisfied. Then from and Theorem 5.2, we infer that.

2) Let. Thus there exists

such that

(5.15)

So, from and item (1), the result follows if we can show that. It follows from that and there exists such that. Hence from (5.15), we see that, that is,.

Remark 5.1 The irreducibility condition in Corollary 5.1 cannot be dropped.

Let. Then A is reducible, ,

(as) and, but.

If in Theorem 5.2, we could relax condition (2) in the theorem.

Theorem 5.3 Let, , and let. Assume that

, and. Then.

Proof. Without loss of generality, assume that. Define the diagonal matrix by

Then is nonsingular, and

for all. Thus from, we deduce that

. Hence from Lemma 3.2, we see that.

Remark 5.2 Let, and let be a separation of. It follows from Theorem 4.1 (using the permutation similarity transformation technique) that there exists. It is clear that B satisfies conditions (1) and (2) of Theorem 5.2 as well. So, from

and Theorem 5.2, we deduce that. This obser- vation together with (3.8) lead to the following corollary.

Corollary 5.2 Let. Then is a pair of incom- parable classes.

The following corollary establishes the first inclusion of (3.3).

Corollary 5.3 Let, and let be a separation of. Then.

Proof. Let. Then from (iv) of item (4) of Remark 3.1, we deduce that there exist and such that (2.4) and (3.1) are satisfied. Thus condition (1) of Theorem 5.2 is satisfied. Also, A satisfies condition (2) of Theorem 5.2 by virtue of being irreducible. Hence from

and item (2) of Theorem 5.2, we infer that, where is the nonsingular diagonal matrix defined by (5.7) and (5.8). Also, since and satisfy (2.4), we see from item (3) of Theorem 5.2 that. Finally, from and being nonsingular diagonal matrix, we deduce that. This completes the proof that, that is,.

It follows from (v) of item (4) of Remark 3.1 that in order to establish sufficient conditions for matrices in, , to be in, it suffices to provide such conditions for matrices in. In the following theorem, if a set is empty its maximum is understood to be 0.

Theorem 5.4 Let, , and let be a separation of. Let be a diagonal matrix in with positive diagonal entries such that. Assume that A and satisfy the following conditions:

Condition (1):.

Condition (2): for all.

Condition (3): For all, we have and

.

Then

1) For every, we have.

2) If and, then and

.

3) If A and satisfy the additional condition:

Condition (4):

then.

Proof. We first observe that the existence of the diagonal matrix with positive diagonal entries, which satisfies, is ensured by virtue of and Lemma 3.2.

1) Let. Since, we deduce from condition (2) that.

2) Let, and assume that. Then from condition (3),

and, we infer that and

.

3) Assume that A and also satisfy condition (4). We first observe that the condition is logically viable by virtue of condition (2) and items (1) and (2). It follows from condition (1) that (2.3) is satisfied for all and. Also, from conditions (1) and (2), we infer that (2.3) is satisfied for all and with. Thus, it remains to consider the case and with. It follows from condition (3) and item (2) that

Hence from condition (4), we see that (2.3) also holds for all and with.

Example 5.1 Let, and let

and. Then and, with, we see that and conditions (1)-(4) of Theorem 5.4 are satisfied with

Then.

6. Row-Column Diagonally Dominant Matrices with Index α vs. Matrices with Other Variants of the Diagonal Dominance Property

In this section, we investigate the relations between the class

and the other classes introduced in Definition 2.1. There has not been too much attention in the literature to discuss such relations.

For a matrix, , define the sets, , , and by

(6.1)

It is clear that is decomposed into the three mutually disjoint sets

, and. Theorem 6.2 investigates the relation between the classes and. A characterization of the class is given in Theorem 5 of [27] . We will use the following slightly modified version of the result in Theorem 6.2.

Theorem 6.1 Let,. Define the sets and

by (6.1). Then the following statements hold:

1) If A satisfies the condition

(6.2)

then

(6.3)

2) for some if and only if A satisfies condition (6.2) and the condition:

(6.4)

Also, if A satisfies conditions (6.2) and (6.4), then the reals and defined by

(6.5)

satisfy and for all.

Theorem 6.2 Let. Then

Proof. Let. Then A satisfies condition (6.2). Also, from and the definition of (in (6.1)), we get

(6.6)

As A satisfies (6.2), we deduce from item (1) of Theorem 6.1 that A satisfies (6.3). Thus from (6.6), we infer that A satisfies (6.4) and the real defined by the first equality of (6.5) satisfies. Hence from the fact that A satisfies (6.2) and item (2) of Theorem 6.1, we see that for all

, where is the real defined by the second equality of (6.5).

Remark 6.1 There is no set inclusion between the classes and, or between the classes and as the one established in Theorem 6.2 between the classes and. However, Theorem 6.3 provides sufficient conditions for matrices in the classes and to be in the classes and, respectively.

We will use in Theorem 6.3 and other parts in the section the following remark.

Remark 6.2 Let, and let be the function defined by for all. Then is continuous. Moreover,

1) If, then is strictly decreasing and.

2) If, then is constant and.

3) If, then is strictly increasing and.

Theorem 6.3 Let, and let. Assume that A satisfies the following condition:

Condition (1): There exists a nonempty subset S of such that for every,

(6.7)

Then

1) For each, we have for all.

2) If and then.

3) If and then.

Proof. 1) Let, and let. Since

we deduce from (6.7) that it remains to consider the case: . In this case, we infer from Remark 6.2 that and. Then holds.

2) The result follows from item (1).

3) The result follows from item (1).

The following theorem discusses the relation between the classes

and

.

Theorem 6.4 Let, and let be a separation of. Then

1).

2) We have

3) If and, then,

, and

.

Proof. It follows from Remark 3.4 that it suffices to prove the theorem in the case:, where.

1) Define by

(6.8)

Then. It can be shown by considering the cases

and that

for all and. So,. Also, from (6.8), we have

for all. Then.

2) The result follows from item (1), and Remark 3.1 ((iii) of item (4), and (i) and (ii) of item (6)).

3) Assume that and that. Let be a matrix in, which satisfies the following conditions:

(6.9)

(6.10)

and

(6.11)

The construction of B is possible by virtue of, and

(6.12)

We observe that (6.12) follows from, (6.9) and. As, we have. From (6.10), it is clear that. Also, it follows from (6.11) that. This proves

. It then follows from Remark 3.1 ((ii) and (iii) of item (4), and (ii) of item (6)) that the remaining statements hold.

Remark 6.3 It is clear that the irreducible matrix A defined in item (1) of Theorem 6.4 satisfies. Then from, and (ii) and (iii) of item (4) of Remark 3.1, we see that the inclusions in (v) of item (4) of Remark 3.1 and Lemma 3.1 are all proper.

Let. In Examples 6.1 and 6.2, we construct a matrix B which satisfies conditions (6.9)-(6.11). The case is considered in Example 6.1, while the case is considered in Example 6.2.

Example 6.1 Let. Define by

Then, and

So,. From (i) of item (4) of Remark 3.1, it is clear that.

Example 6.2 Let, and let be such that

. Define by

Then, and

So,.

Theorem 6.5 investigates the relations between the class

and each of the classes

and.

Theorem 6.5 Let. Then

1).

2),

and

.

3) If and, then,

, and

.

4) If, then.

Proof. 1) Define the matrix A by

(6.13)

and define by

(6.14)

where A is given by (6.13) and and are given by

(6.15)

and

(6.16)

It follows from (6.13) - (6.16) that, and with defined by

we have. Also, since for all, we deduce from (6.13)-(6.16) that.

2) The statements follow from item (1), and items (1)-(3) and (6) of Remark 3.1.

3) Let, and let. Let be a matrix in

, which satisfies the following condition:,. (Such matrix exists; see item (3) of Theorem 6.4.) Then

. It then follows from items (2), (3) and (6) of Remark 3.1 that the remaining statements also hold.

4) Let. Define by and for all

. Then.

Remark 6.4 Let. It is clear that the matrix

defined in item (1) of Theorem 6.5 satisfies. Then from, and

, we see that the respective inclusions,

and in item (1) of Remark 3.1 are all proper.

Remark 6.5 We are not able to determine whether or. However, we show in Theorem 6.6 that a subclass of containing is indeed a subclass of

. The theorem also establishes.

Definition 6.1 Let, and let. Define the class by

(6.17)

For every, define the function by

(6.18)

for all. Also, define the class by

(6.19)

To simplify notation, we denote for every, the matrix

by.

Theorem 6.6 Let, and let. Then

1).

2) If and is a positive eigenvector of, then the diagonal matrix satisfies

(6.20)

for all.

3), and, and the three inclusions are proper.

4).

Proof. 1) Let. Then for all. Thus from (6.17), we deduce that. Also, from and (6.18), it is clear that (see Definition 6.1) is both nonnegative and irreducible. Hence from Theorem 8.4.4 of [26] , we infer that has a positive eigenvector. Then from and (6.19), we see that.

2) Let, and let be a positive eigenvector of. Thus from (see Definition 6.1) and Corollary 8.1.30 of [26] , we deduce that the eigenvalue of corresponding to the positive eigenvector of is. Hence from the definition of, we get

(6.21)

for all. It follows from (in (3.4)) and (6.18) that for each matrix, we have

(6.22)

Let. Then from

(6.18) and the definition of, we obtain for all

. Thus from being singular (as is an eigenvalue of) and (6.22), we infer that there exists such that

. Hence from the definitions of and, we

see that. Then from (6.18) and (6.21), we deduce that with

, inequality (6.20) holds for all.

3) We prove. The other two set inclusions are proven similarly. Let. Thus from the definition of, there exists a positive eigenvector of. Hence from item (2), we infer that, with, inequality (6.20) is satisfied for all. Then from and,

, we see that. Thus from Lemma 3.2, we deduce that.

It follows from Remark 3.1 (item (1), and (ii) of item (6)) that in order to show that the three set inclusions are proper, it suffices to show that there exists such that. Define by

(6.23)

Hence. Also, with, and

for all, we deduce from (6.23) that. So, from, the result follows.

4) The result follows from in item (3), and item (1) of Lemma 3.3.

We now provide sufficient conditions for matrices in the classes, and to be in the classes, and, respectively. It follows from Theorems 6.2 and 6.3 that in order to establish such conditions, it suffices to consider matrices in the smaller classes, and. The integer n in Theorems 6.7-6.9 is assumed to satisfy.

Theorem 6.7 Let, and let l be the integer in, which satisfies. Assume that A satisfies the following two conditions:

Condition (1): Every satisfies (6.7).

Condition (2): Either, or and.

Then there exists such that.

Proof. Since for all, we deduce from condition (1) and item (1) of Theorem 6.2 that

(6.24)

for all and. It is clear that

(6.25)

Then from condition (2), it remains to consider the case in which l satisfies the conditions and. In this case, we infer from Remark 6.2 that there exist and such that

(6.26)

for all. Since, we see from Remark 6.2 that the function, , is an increasing function. Thus from (6.26) and, we see that for all. Hence from (6.24) and (6.25), the result follows.

The following two theorems are proven similarly as Theorem 6.7.

Theorem 6.8 Let, and let m be the integer in, which satisfies. Assume that A satisfies the following two condition:

Condition (1): Every satisfies (6.7).

Condition (2): Either, or and

.

Then there exists such that.

It follows from item (4) of Lemma 3.3 that

. We use this fact in the following theorem. We omit the proof.

Theorem 6.9 Let, and let. Suppose that l is the integer in, which satisfies. Assume that A satisfies the following two conditions:

Condition (1): For every, we have.

Condition (2): and.

Then there exists such that

In particular,.

Remark 6.6 If in Theorem 6.8, the fact:

for all follows from (as

).

Remark 6.7 1) Theorems 5.4 and 6.6 could be used to establish sufficient conditions for matrices in to be in.

2) Theorem 4.5, item (2) of Remark 4.2, and Theorems 6.7-6.9 could be used to present sufficient conditions for matrices in, and to be in, and, respectively.

3) Theorems 4.5, 5.4 and 6.6 could be used to provide sufficient conditions for matrices in to be in.

Acknowledgements

The author would like to thank the two referees for their helpful suggestions. The author would also like to thank the library of UBC Okanagan for the research facilities they provided.

Cite this paper

Farid, F.O. (2017) On Classes of Matrices with Variants of the Diagonal Dominance Property. Advances in Linear Algebra & Matrix Theory, 7, 37- 65. https://doi.org/10.4236/alamt.2017.72005

References