A Note on the Spectral Radius of Weighted Signless Laplacian Matrix
Vol.08No.01(2018), Article ID:83136,11 pages
10.4236/alamt.2018.81006
Şerife Büyükköse1, Nurşah Mutlu1, Gülistan Kaya Gök2
1Departments of Mathematics, Faculty of Sciences, Gazi University, Ankara, Turkey
2Department of Mathematics Education, Hakkari University, Hakkari, Turkey
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 6, 2017; Accepted: March 17, 2018; Published: March 20, 2018
ABSTRACT
A weighted graph is a graph that has a numeric label associated with each edge, called the weight of edge. In many applications, the edge weights are usually represented by nonnegative integers or square matrices. The weighted signless Laplacian matrix of a weighted graph is defined as the sum of adjacency matrix and degree matrix of same weighted graph. In this paper, a brief overview of the notation and concepts of weighted graphs that will be used throughout this study is given. In Section 2, the weighted signless Laplacian matrix of simple connected weighted graphs is considered, some upper bounds for the spectral radius of the weighted signless Laplacian matrix are obtained and some results on weighted and unweighted graphs are found.
Keywords:
Weighted Graph, Weighted Signless Laplacian Matrix, Spectral Radius

1. Introduction
A weighted graph is a graph that has a numeric label associated with each edge, called the weight of edge. In many applications, the edge weights are usually represented by nonnegative integers or square matrices. In this paper, we generally deal with simple connected weighted graphs where the edge weights are positive definite square matrices. Let be a simple connected weighted graph with vertex set . Let be the positive definite weight matrix of order t of the edge ij and assume that . The weight of a vertex defined as ; where denotes the vertex j is adjacent to i.
Unless otherwise specified, by a weighted graph we mean a graph with each edge weight is a positive definite square matrix.
The weighted signless Laplacian matrix of weighted graph G is a block matrix and defined as , where
Clearly, is a square matrix of order nt. The eigenvalues may be denoted by , where . Also let , and denote the spectral radius of G and the largest eigenvalues of and , respectively. If is the weighted adjacency matrix of G, then note that
,
where .
In literature, there are a lot of studies deal with upper and lower bounds for the spectral radius of signless Laplacian matrix of unweighted graphs. For a simple connected and unweighted graph G, there are some known upper bounds on the spectral radius of signless Laplacian matrix as follows such that is
degree of vertex i and .
, (1)
, (2)
, (3)
, (4)
. (5)
In this paper, some upper bounds for the spectral radius of signless Laplacian matrix of weighted graphs are given. Also some results on weighted and unweighted graphs are obtained by using these bounds. The following lemmas are convenient for the graphs we consider.
Lemma 1. [1] .
If A is a real symmetric matrix with eigenvalues , then for any ,
.
The equality holds if and only if is an eigenvector of A corresponding to the least eigenvalue .
Lemma 2. [2] .
If A is a real symmetric matrix with eigenvalues then for any , ,
.
The equality holds if and only if is an eigenvector of A corresponding to the largest eigenvalue and for some .
Lemma 3. [3] .
Let G be a weighted graph and let be the positive definite weight matrix of order t of the edge ij. Also let be an eigenvector of corresponding to the largest eigenvalue for all i, j. Then
.
Lemma 4. [4] .
Let G be a weighted graph and let be the positive definite weight matrix of order t of the edge ij. If and are not Hermitian matrices for all j, j∼i and for all k, k∼j, j∼i, then for any , ,
2. Main Results
In this section, some upper bounds for the spectral radius of weighted signless Laplacian matrix are found.
Theorem 5.
Let be a simple connected weighted graph. Then
. (6)
Proof.
Let be an eigenvector corresponding to the eigenvalue
and be the vector component of such that
. (7)
Since is nonzero, so is . We have
. (8)
From the i-th Equation of (8), we get
,
i.e.,
.
From (7) and using Lemma 2, we get
.
From Lemma 1 and Lemma 3, we have
.
Thus
.
Hence the theorem follows.
Corollary 6.
Let G be a simple connected weighted graph where each edge weight is a positive number. Then
.
Proof.
For weighted graphs where the edge weights are positive number, we have and , for all . Using Theorem 5 we get the required result.
Corollary 7. [5] .
Let G be a simple connected unweighted graph. Then
,
where is the degree of vertex i.
Proof.
For an unweighted graph, and for all and . Using Corollary 6 we get the required result.
Theorem 8.
Let G be a simple connected weighted graph. Then
. (9)
Proof.
Let us consider the matrix . The -th element of is
Let be an eigenvector corresponding to the eigenvalue of and be the vector component of such that
. (10)
Since is nonzero, so is . We have
. (11)
From the i-th Equation of (11), we get
,
i.e.,
.
From (10) and using Lemma 1 and Lemma 2, we get
(12)
Thus
.
Hence the theorem follows.
Corollary 9.
Let G be a simple connected weighted graph where each edge weight is a positive number. Then
.
Proof.
For weighted graphs where the edge weights are positive number, we have and , for all . Using Theorem 8 we get the required result.
Corollary 10. [6] .
Let G be a simple connected unweighted graph. Then
,
where is the degree of vertex i.
Proof.
For an unweighted graph, and for all and . Using Corollary 9 we get the required result.
Theorem 11.
Let G be a simple connected weighted graph. Then,
, (13)
where
Proof.
From (12), we get
The proof is complete.
Corollary 12.
Let G be a simple connected weighted graph where each edge weight  is a positive number. Then
is a positive number. Then
 ,
,
where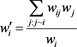 .
.
Proof.
For weighted graphs where the edge weights 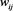 are positive number, we have
are positive number, we have 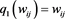 and
and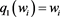 , for all
, for all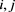 . Using Theorem 11 we get the required result.
. Using Theorem 11 we get the required result.
Corollary 13. [6] .
Let G be a simple connected unweighted graph. Then
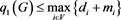 ,
,
where 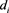 is the degree of vertex i and
is the degree of vertex i and 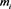 is the average of the degrees of the vertices adjacent to vertex i.
is the average of the degrees of the vertices adjacent to vertex i.
Proof.
For an unweighted graph, 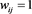 and
and 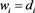 for all
for all 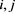 and
and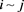 . Using Corollary 12 we get the required result.
. Using Corollary 12 we get the required result.
Theorem 14.
Let G be a simple connected weighted graph. Then
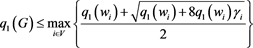 , (14)
, (14)
where 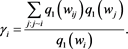
Proof.
Let 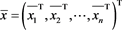 be an eigenvector corresponding to the eigenvalue
be an eigenvector corresponding to the eigenvalue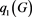 . We assume that
. We assume that  be the vector component of
be the vector component of  such that
such that
 . (15)
. (15)
Since  is nonzero, so is
is nonzero, so is . We have
. We have

In order to prove the Inequality (14), we consider a simple quadratic function of :
:
 (16)
(16)
From the i-th Equation of (16), we get

i.e.,

Since  is the positive definite matrix of edge ij,
is the positive definite matrix of edge ij,  matrix is also positive definite. From Lemma 1, we have
matrix is also positive definite. From Lemma 1, we have
 (17)
(17)
Four cases arise;
1) 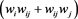 and
and  are real symmetric matrices for all j, j∼i and for all k, k∼j, j∼i.
are real symmetric matrices for all j, j∼i and for all k, k∼j, j∼i.
2)  is a real symmetric matrix for all j, j∼i and
is a real symmetric matrix for all j, j∼i and  is not a real symmetric matrix for all k, k∼j, j∼i.
is not a real symmetric matrix for all k, k∼j, j∼i.
3)  is not a real symmetric matrix for all j, j∼i and
is not a real symmetric matrix for all j, j∼i and  is a real symmetric matrix for all k, k∼j, j∼i.
is a real symmetric matrix for all k, k∼j, j∼i.
4)  and
and 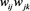 are not real symmetric matrices for all j, j∼i and for all k, k∼j, j∼i.
are not real symmetric matrices for all j, j∼i and for all k, k∼j, j∼i.
From (15), (17) and using Lemma 2 and Lemma 4, we get
 (18)
(18)
for Case (1), Case (2), Case (3) and Case (4). Hence,

From Lemma 3, we have

i.e.,

Thus

From the inequality above, for every different value to b, we can get several distinct upper bounds. In particular, if , we get
, we get
 .
.
This completes the proof.
Corollary 15.
Let G be a simple connected weighted graph where each edge weight  is a positive number. Then
is a positive number. Then
 ,
,
where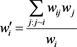 .
.
Proof.
For weighted graphs where the edge weights  are positive number, we have
are positive number, we have  and
and , for all
, for all . Using Theorem 14 we get the required result.
. Using Theorem 14 we get the required result.
Corollary 16. [5] .
Let G be a simple connected unweighted graph. Then
 ,
,
where  is the degree of vertex i and
is the degree of vertex i and  is the average of the degrees of the vertices adjacent to vertex i.
is the average of the degrees of the vertices adjacent to vertex i.
Proof.
For an unweighted graph,  and
and  for all
for all  and
and . Using Corollary 15 we get the required result.
. Using Corollary 15 we get the required result.
Theorem 17.
Let G be a simple connected weighted graph. Then,
 , (19)
, (19)
where 
Proof.
 . The
. The  -th element of
-th element of  is
is

Let  be an eigenvector corresponding to the eigenvalue
be an eigenvector corresponding to the eigenvalue  of
of ,
,  and
and  are the vector components of
are the vector components of  such that
such that
 , (20)
, (20)
 . (21)
. (21)
Since  is nonzero, so is
is nonzero, so is . We have
. We have
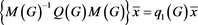 . (22)
. (22)
From the i-th Equation of (22), we get
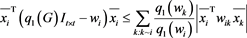 .
.
From Lemma 2, we get
 . (23)
. (23)
From (21), (23) and using Lemma 1, we get
 (24)
(24)
Similarly, from the j-th Equation of (22), we have
 (25)
(25)
From (24) and (25), we get

Thus
 .
.
Hence the theorem is proved.
Corollary 18.
Let G be a simple connected weighted graph where each edge weight  is a positive number. Then
is a positive number. Then
 ,
,
where .
.
Proof.
For weighted graphs where the edge weights  are positive number, we have
are positive number, we have  and
and , for all
, for all . Using Theorem 17 we get the required result.
. Using Theorem 17 we get the required result.
Corollary 19. [7] .
Let G be a simple connected unweighted graph. Then
 ,
,
where  is the degree of vertex i and
is the degree of vertex i and  is the average of the degrees of the vertices adjacent to vertex i.
is the average of the degrees of the vertices adjacent to vertex i.
Proof.
For an unweighted graph,  and
and  for all
for all  and
and . Using Corollary 18 we get the required result.
. Using Corollary 18 we get the required result.
Conflict of Interests
The authors declare that there is no conlict of interests regarding the publication of this paper.
Cite this paper
Büyükköse, Ş., Mutlu, N. and Gök, G.K. (2018) A Note on the Spectral Radius of Weighted Signless Laplacian Matrix. Advances in Linear Algebra & Matrix Theory, 8, 53-63. https://doi.org/10.4236/alamt.2018.81006
References
- 1. Zhang, F. (1999) Matrix Theory: Basic Results and Techniques. Springer-Verlag, New York. https://doi.org/10.1007/978-1-4757-5797-2
- 2. Horn, R.A. and Johnson, C.R. (1985) Matrix Analysis. Cambridge University Press, New York. https://doi.org/10.1017/CBO9780511810817
- 3. Das, K.C. (2007) Extremal Graph Characterization from the Upper Bound of the Laplacian Spectral Radius of Weighted Graphs. Linear Algebra and Its Applications, 427, 55-69. https://doi.org/10.1016/j.laa.2007.06.018
- 4. Büyükköse, Ş. and Mutlu, N. (2015) The Upper Bound for the Largest Signless Laplacian Eigenvalue of Weighted Graphs. Gazi University Journal of Science, 28, 709-714.
- 5. Oliveira, C.S., Lima, L.S., Abreu, N.M. and Hansen, P. (2010) Bounds on the Index of the Signless Laplacian of a Graph. Discrete Applied Mathematics, 158, 355-360. https://doi.org/10.1016/j.dam.2009.06.023
- 6. Anderson, W.N. and Morley, T.D. (1985) Eigenvalues of the Laplacian of a Graph. Linear and Multilinear Algebra, 18, 141-145. https://doi.org/10.1080/03081088508817681
- 7. Das, K.C. (2004) A Characterization on Graphs Which Achieve the Upper Bound for the Largest Laplacian Eigenvalue of Graphs. Linear Algebra and Its Applications, 376, 173-186. https://doi.org/10.1016/j.laa.2003.06.009
上一篇:Jordan Γ*-Derivation on 下一篇:Extending Kantorovich-Type Ine
最新文章NEWS
- On Characterization of Poised Nodes for a Space of Bivariate Functions
- Least-Squares Solutions of Generalized Sylvester Equation with Xi Satisfies Different Linear Constra
- Matrices and Division by Zero z/0 = 0
- Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution
- Two Nonzero Component Lemma and Matrix Trigonometry
- Using Row Reduced Echelon Form in Balancing Chemical Equations
- Tight Monomials with t-Value ≤ 9 for Quantum Group of Type D4
- Minimum Covering Randić Energy of a Graph
推荐期刊Tui Jian
- Chinese Journal of Integrative Medicine
- Journal of Genetics and Genomics
- Journal of Bionic Engineering
- Pedosphere
- Chinese Journal of Structural Chemistry
- Nuclear Science and Techniques
- 《传媒》
- 《中学生报》教研周刊
热点文章HOT
- Using Row Reduced Echelon Form in Balancing Chemical Equations
- Minimum Covering Randić Energy of a Graph
- A Note on the Inclusion Sets for Tensors
- A General Hermitian Nonnegative-Definite Solution to the Matrix Equation AXB = C
- Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution
- Matrices and Division by Zero z/0 = 0
- On Characterization of Poised Nodes for a Space of Bivariate Functions
- Pseudo Laguerre Matrix Polynomials, Operational Identities and Quasi-Monomiality
