A Cauchy Problem for Some Fractional q-Difference Equations with Nonlocal Conditions
Vol.06No.02(2016), Article ID:67792,7 pages
10.4236/ajcm.2016.62017
Maryam Al-Yami
Al Faisaliah Campus, Sciences Faculty, King Abdulaziz University, Jeddah, Saudi Arabia

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2016; accepted 26 June 2016; published 29 June 2016
ABSTRACT
In this paper, we discussed the problem of nonlocal value for nonlinear fractional q-difference equation. The classical tools of fixed point theorems such as Krasnoselskii’s theorem and Banach’s contraction principle are used. At the end of the manuscript, we have an example that illustrates the key findings.
Keywords:
Cauchy Problem, Fractional q-Difference Equation, Nonlocal Conditions, Fixed Point, Krasnoselskii’s Theorem

1. Introduction
Importance of fractional differential equations appears in many of the physical and engineering phenomena in the last two decades [1] - [3] . Problems with nonlocal conditions and related topics were studied in, for example [4] , and the nonlocal Cauchy problem [5] . The attention of researchers subject of q-difference equations appeared in recent years [6] [7] . Initially, it was developed by Jackson [8] [9] . Noted recently the attention of many researchers is in the field of fractional q-calculus [10] [11] . Recently nonlocal fractional q-difference problems have aroused considerable attention [12] [13] .
In this paper, we obtain the results of the existence and uniqueness of solutions for the Cauchy problem with nonlocal conditions for some fractional q-difference equations given by
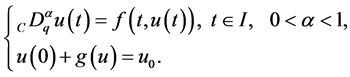 (1)
(1)
Here, 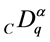 is the Caputo fractional q-derivative of order
is the Caputo fractional q-derivative of order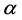 ,
, 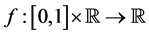 and
and 
are given continuous functions. It is worth mentioning that the nonlocal condition  which can be applied effectively in physics is better than the classical Cauchy problem condition
which can be applied effectively in physics is better than the classical Cauchy problem condition , see [14] .
, see [14] .
Several authors have studied the semi-linear differential equations with nonlocal conditions in Banach space, [15] [16] . In [17] , Dong et al. studied the existence and uniqueness of the solutions to the nonlocal problem for the fractional differential equation in Banach space. Motivated by these studied, we explore the Cauchy problem for nonlinear fractional q-difference equations according to the following hypotheses.
(H1)  is jointly continuous.
is jointly continuous.
(H2) 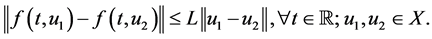
(H3) 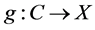 is continuous and
is continuous and 
(H4)  where
where 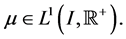
The problem (1) is then devolved to the following formula
 (2)
(2)
See reference [18] for more details.
2. Preliminaries on Fractional q-Calculus
Let 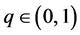 and define
and define

The q-analogue of the Pochhammer symbol was presented as follows

In general, if  thereafter
thereafter

The q-gamma function is defined by

and satisfies 
The q-derivative of a function  is here defined by
is here defined by

and

The q-integral of a function f defined in the interval  is provided by
is provided by

Now, it can be defined an operator , as follows
, as follows
 and
and 
We can point to the basic formula which will be used at a later time,

where  denotes the q-derivative with respect to variable s.
denotes the q-derivative with respect to variable s.
See reference [7] - [10] for more details.
Definition 2.1. [19] Let  and f be a function defined on
and f be a function defined on . The fractional q-integral of the Riemann-Liouville type is
. The fractional q-integral of the Riemann-Liouville type is  and
and

Definition 2.3. [19] The fractional q-derivative of the Caputo type of order  is defined by
is defined by

where  is the smallest integer greater than or equal to
is the smallest integer greater than or equal to .
.
Theorem 2.1. [20] Let  and
and .Then, the following equality holds
.Then, the following equality holds

Theorem 2.2. [18] [19] (Krasnoselskii)
Let M be a closed convex non-empty subset of a Banach space . Suppose that A and B maps M into X, such that the following hypotheses are fulfilled:
. Suppose that A and B maps M into X, such that the following hypotheses are fulfilled:
1)  for all
for all ;
;
2) A is continuous and AM is contained in a compact set;
3) B is a contraction mapping.
Then there exists  such that
such that 
3. Main Results
Now, the obtained results are presented.
Theorem 3.1.
Let (H1)- (H3) hold, if  and
and , the problem (1) has a unique solution.
, the problem (1) has a unique solution.
Proof. Define  by
by

Choose  and let
and let . So, we can prove that
. So, we can prove that , where
, where
 . For it, let
. For it, let  and
and . Consequently, we find that
. Consequently, we find that

This shows that  therefore,
therefore, .
.
Now, for , we obtain
, we obtain

Thus
 ,
,
where 
Thus, by the Banach’s contraction mapping principle, we find that the problem (1) has a unique solution.
Our next results are based on Krasnoselskii’s fixed-point theorem.
Theorem 3.2.
Let (H1), (H2), (H3) with  and (H4) hold, then the problem (1) has at least one solution on I.
and (H4) hold, then the problem (1) has at least one solution on I.
Proof. Take , and consider
, and consider 
Let A and B the two operators defined on P by

and

respectively. Note that if  then
then

Thus 
By (H2), it is also clear that B is a contraction mapping.
Produced from Continuity of u, the operator  is continuous in accordance with (H1). Also we observe that
is continuous in accordance with (H1). Also we observe that

Then A is uniformly bounded on P.
Now, let  and
and  That’s where f is bounded on the compact set
That’s where f is bounded on the compact set  it means
it means
 We will get
We will get

which is autonomous of u and head for zero as  Consequently, A is equicontinuous. Thus, A is relatively compact on P. Therefore, according to the Arzela-Ascoli Theorem, A is compact on P. Thus, the problem (1) has at least one solution on I.
Consequently, A is equicontinuous. Thus, A is relatively compact on P. Therefore, according to the Arzela-Ascoli Theorem, A is compact on P. Thus, the problem (1) has at least one solution on I.
Example 4.1 Consider the following nonlocal problem
 (3)
(3)
where 
Set

and

Let  and
and  Then we have
Then we have

and

It is obviously that our assumptions in Theorem 3.1 holds with  and for appropriate values of
and for appropriate values of  with
with  and
and  Indeed
Indeed
 (4)
(4)
Therefore the problem (3) has a unique solution on  for values of
for values of  and q sufficient stipulation (4). For illustration
and q sufficient stipulation (4). For illustration
・ If  and
and  then
then  and
and 
・ If  and
and  then
then  and
and 
Cite this paper
Maryam Al-Yami, (2016) A Cauchy Problem for Some Fractional q-Difference Equations with Nonlocal Conditions. American Journal of Computational Mathematics,06,159-165. doi: 10.4236/ajcm.2016.62017
References
- 1. Campos, L.M.B.C. (1990) On the Solution of Some Simple Fractional Differential Equations. International Journal of Mathematics and Mathematical Sciences, 13, 481-496.
http://dx.doi.org/10.1155/S0161171290000709 - 2. Diethelm, K. and Ford, N.J. (2002) Analysis of Fractional Differential Equations. Journal of Mathematical Analysis and Applications, 265, 229-248.
http://dx.doi.org/10.1006/jmaa.2000.7194 - 3. Kilbas, A.A. and Trujillo, J.J. (2001) Differential Equations of Fractional Order: Methods, Results and Problems, I. Journal of Applied Analysis, 78, 153-192.
http://dx.doi.org/10.1080/00036810108840931 - 4. Furati, K.M. and Tatar, N. (2004) An Existence Result for a Nonlocal Fractional Differential Problem. Journal of Fractional Calculus, 26, 43-51.
- 5. Xiao, F. (2011) Nonlocal Cauchy Problem for Nonautonomous Fractional Evolution Equations. Advances in Difference Equations, 2011, 1-17.
http://dx.doi.org/10.1155/2011/483816 - 6. Ahmad, B. and Nieto, J.J. (2012) On Nonlocal Boundary Value Problems of Nonlinear Q-Difference Equations. Advances in Difference Equations, 81, 1-10.
http://dx.doi.org/10.1186/1687-1847-2012-81 - 7. Kac, V. and Cheung, P. (2002) Quantum Calculus. University Text, Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4613-0071-7 - 8. Jackson, F.H. (1910) On Q-Definite Integrals. The Quarterly Journal of Pure and Applied Mathematics, 41, 193-203.
- 9. Jackson, F.H. (1909) On Q-Functions and a Certain Difference Operator. Transactions of the Royal Society of Edinburgh, 46, 253-281.
http://dx.doi.org/10.1017/S0080456800002751 - 10. Agarwal, R.P. (1969) Certain Fractional Q-Integrals and Q-Derivatives. Proceedings of the Cambridge Philosophical Society, 66, 365-370.
http://dx.doi.org/10.1017/S0305004100045060 - 11. Al-Salam, W.A. (1966) Some Fractional Q-Integrals and Q-Derivatives. Proceedings of the Edinburgh Mathematical Society (Series 2), 15, 135-140.
http://dx.doi.org/10.1017/s0013091500011469 - 12. Ahmad, B.S., Ntouyas, K. and Purnaras, I.K. (2012) Existence Results for Nonlocal Boundary Value Problems of Nonlinear Fractional Q-Difference Equations. Advances in Difference Equations, 140, 1-15.
- 13. Zhao, Y., Chen, H. and Zhang, Q. (2013) Existence Results for Fractional Q-Difference Equations with Nonlocal Q-Integral Boundary Conditions. Advances in Difference Equations, 84, 1-15.
http://dx.doi.org/10.1016/j.jde.2013.03.005 - 14. Deng, K. (1993) Exponential Decay of Solutions of Semilinear Parabolic Equations with Nonlocal Initial Conditions. Journal of Mathematical Analysis and Applications, 179, 630-637.
http://dx.doi.org/10.1006/jmaa.1993.1373 - 15. Chen, L. and Fan, Z. (2011) On Mild Solutions to Fractional Differential Equations with Nonlocal Conditions. Electronic Journal of Qualitative Theory of Differential Equations, 53, 1-13.
http://dx.doi.org/10.14232/ejqtde.2011.1.53 - 16. N’Guérékata, G.M. (2006) Existence and Uniqueness of an Integral Solution to Some Cauchy Problem with Nonlocal Conditions, Differential & Difference Equations and Applications. Hindawi Publishing Corp., New York, 843-849.
- 17. Dong, X., Wang, J. and Zhou, Y. (2011) On Nonlocal Problems for Fractional Differential Equations in Banach Spaces. Opuscula Mathematica, 31, 341-357.
http://dx.doi.org/10.7494/OpMath.2011.31.3.341 - 18. Smart, D.R. (1974) Fixed Point Theorems. Cambridge Tracts in Mathematics, No. 66. Cambridge University Press, London, New York.
- 19. Stanković, M.S., Rajković, P.M. and Marinković, S.D. (2009) On Q-Fractional Derivatives of Riemann-Liouville and Caputo Type. arXiv Preprint arXiv:0909.0387.
- 20. Annaby, M.H. and Mansour, Z.H. (2012) Q-Fractional Calculus. Vol. 2056, Springer, Berlin.
上一篇:On the Location of Zeros of Po 下一篇:On Existence of Solutions of q
最新文章NEWS
- Auto-Bäcklund Transformation and Extended Tanh-Function Methods to Solve the Time-Dependent Coeffici
- A Third-Order Scheme for Numerical Fluxes to Guarantee Non-Negative Coefficients for Advection-Diffu
- Conjugate Effects of Radiation and Joule Heating on Magnetohydrodynamic Free Convection Flow along a
- An O(k<sup>2</sup>+kh<sup>2</sup>+h<sup>2</sup>) Accurate Two-le
- On the Location of Zeros of Polynomials
- Peristaltic Pumping of a Conducting Sisko Fluid through Porous Medium with Heat and Mass Transfer
- An Accurate Numerical Integrator for the Solution of Black Scholes Financial Model Equation
- Simulation of Time-Dependent Schrödinger Equation in the Position and Momentum Domains
推荐期刊Tui Jian
- Chinese Journal of Integrative Medicine
- Journal of Genetics and Genomics
- Journal of Bionic Engineering
- Pedosphere
- Chinese Journal of Structural Chemistry
- Nuclear Science and Techniques
- 《传媒》
- 《中学生报》教研周刊
热点文章HOT
- Asymptotic Solutions for the Fifth Order Critically Damped Nonlinear Systems in the Case for Small E
- Partial Fraction Decomposition by Repeated Synthetic Division
- Higher-Order Numerical Solution of Two-Dimensional Coupled Burgers’ Equations
- Group Method Analysis of MHD Mixed Convective Flow Past on a Moving Curved Surface with Suction
- Simple and Multi Linear Regression Model of Verbs in Quran
- Conjugate Effects of Radiation and Joule Heating on Magnetohydrodynamic Free Convection Flow along a
- Peristaltic Pumping of a Conducting Sisko Fluid through Porous Medium with Heat and Mass Transfer
- An O(k<sup>2</sup>+kh<sup>2</sup>+h<sup>2</sup>) Accurate Two-le
