The Approximation of Hermite Interpolation on the Weighted Mean Norm
Vol.05No.03(2015), Article ID:59573,6 pages
10.4236/ajcm.2015.53033
Xin Wang1, Chong Hu2, Xiuxiu Ma3
1Department of Mathematics and Computer, Baoding University, Baoding, China
2Institute of Nuclear Technology, China Institute of Atomic Energy, Beijing, China
3Institute of Mathematical, North China Electric Power University, Baoding, China
Email: wangxincloud@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 July 2015; accepted 11 September 2015; published 14 September 2015
ABSTRACT
We research the simultaneous approximation problem of the higher-order Hermite interpolation based on the zeros of the second Chebyshev polynomials under weighted Lp-norm. The estimation is sharp.
Keywords:
Hermite Interpolation Operator, Chebyshev Polynomial, Derivative Approximation

1. Introduction
For 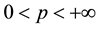 and a non-negative measurable function u, the space
and a non-negative measurable function u, the space 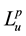 is defined to be the set of measurable
is defined to be the set of measurable 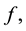 such that
such that

is finite. Of course, when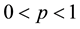 ,
, 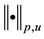 is not a norm; nevertheless, we keep this notation for convenience.
is not a norm; nevertheless, we keep this notation for convenience.
For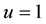 , this is the usual
, this is the usual 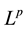 space. For
space. For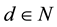 , we write
, we write 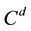 for the space of functions that have dth continuous derivative on
for the space of functions that have dth continuous derivative on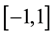 .
.
We introduce a few notations. If 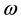 is a Jacobi weight function, we write
is a Jacobi weight function, we write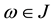 . Let
. Let
 . The Jacobi polynomials
. The Jacobi polynomials 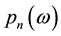 are orthogonal polynomials with respect to the weight function
are orthogonal polynomials with respect to the weight function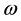 , i.e.
, i.e.

It is well known that  has
has  distinct zeros in
distinct zeros in . These zeros are denoted by
. These zeros are denoted by  and the following order is assumed:
and the following order is assumed:

Later, when we fix , we shall write
, we shall write  instead of
instead of .
.
For a given integer  and
and , the Hermite interpolation is defined to be the unique polynomial of degree
, the Hermite interpolation is defined to be the unique polynomial of degree , denoted by
, denoted by , satisfying
, satisfying

for , where
, where , if
, if  or
or  then we have no interpolation at 1 or −1. We shall fix the integers
then we have no interpolation at 1 or −1. We shall fix the integers  and
and  for the rest of the paper, and omit them from the notations. Thus, for example, we shall write
for the rest of the paper, and omit them from the notations. Thus, for example, we shall write  instead of
instead of . Let
. Let

Vertesi and Xu [1] , Nevai and Xu [2] , and Pottinger considered the simultaneous approximation by Hermite interpolation operators.
We have researched the simultaneous approximation problem of the lower-order Hermite interpolation based on the zeros of Chebyshev polynomials under weighted Lp-norm in references [3] -[5] . We will research the simultaneous approximation problem of the higher-order Hermite interpolation in this article.
Let

be the zeros of , the nth degree Chebyshev polynomial of the second kind. For
, the nth degree Chebyshev polynomial of the second kind. For
 , let
, let  be the polynomial of degree at most 3n − 1 which satisfies
be the polynomial of degree at most 3n − 1 which satisfies

Then the Hermite interpolation polynomial is given by
 (1.1)
(1.1)
where
 (1.2)
(1.2)
 (1.3)
(1.3)
 (1.4)
(1.4)
 (1.5)
(1.5)
Theorem 1.
Let  be defined as (1.1), for
be defined as (1.1), for  and
and , then we have
, then we have

2. Some Lemmas
Lemmas 1. [6] Let  be defined as (1.1), then
be defined as (1.1), then

where ,
,  ,
,  is defined as function
is defined as function  at
at  before the commencement of the Taylor series of
before the commencement of the Taylor series of .
.
Lemma 2. [7]
If , then there exists a algebraic polynomial
, then there exists a algebraic polynomial  of degree at most
of degree at most  such that
such that

Let

be the zeros of , here
, here , the nth degree Chebyshev polynomial of
, the nth degree Chebyshev polynomial of
the second kind. For , the well-known Lagrange interpolation polynomial of
, the well-known Lagrange interpolation polynomial of  based on
based on  is given by
is given by
 (2.1)
(2.1)
where
 (2.2)
(2.2)
 (2.3)
(2.3)
 (2.4)
(2.4)
Lemma 3. [7] Let  be defined as (2.4), for
be defined as (2.4), for , and
, and , we have
, we have

3. The Proof of Theorem 1
For , let
, let  be the polynomial of degree at most
be the polynomial of degree at most  which satisfies Lemma 2. By the uniqueness of Hemite interpolation polynomial, it can be easily checked that,
which satisfies Lemma 2. By the uniqueness of Hemite interpolation polynomial, it can be easily checked that,
 (3.1)
(3.1)
We can conclude that
 (3.2)
(3.2)
Firstly, we estimate . By (3.1), we have
. By (3.1), we have
 (3.3)
(3.3)
Firstly, we estimate ,
,
 (3.4)
(3.4)
Let
 (3.5)
(3.5)
be the polynomial of degree . By the uniqueness of Lagrange interpolation polynomial, it can be easily checked that,
. By the uniqueness of Lagrange interpolation polynomial, it can be easily checked that,
 (3.6)
(3.6)
By (3.5), (3.6) and Lemma 3, we can derive
 (3.7)
(3.7)
Firstly, we estimate . Let
. Let
 (3.8)
(3.8)
then
 (3.9)
(3.9)
From Lemma 2 and (3.8), (3.9), we have that for 
 (3.10)
(3.10)
For , we have
, we have
 (3.11)
(3.11)
We can conclude
 (3.12)
(3.12)
Secondly, we estimate , and by Lemma 2, we get
, and by Lemma 2, we get
 (3.13)
(3.13)
Similarly
 (3.14)
(3.14)
By (3.12), (3.13) and (3.14), we have
 (3.15)
(3.15)
Similarly, we get
 (3.16)
(3.16)
 (3.17)
(3.17)
By (3.15), (3.16) and (3.17), we get
 (3.18)
(3.18)
Similarly, we get
 (3.19)
(3.19)
 (3.20)
(3.20)
Secondly, we estimate , from Lemma 2,
, from Lemma 2,
 (3.21)
(3.21)
From (3.2), (3.3), and (3.21), we can obtain the upper estimate

Funding
Hebei Science and Technology Research Universities Youth Fund project (QN20132001).
Cite this paper
XinWang,ChongHu,XiuxiuMa, (2015) The Approximation of Hermite Interpolation on the Weighted Mean Norm. American Journal of Computational Mathematics,05,387-392. doi: 10.4236/ajcm.2015.53033
References
- 1. Szabados, J. and Vestesi, P. (1992) A Survey on Mean Convergence of Interpolatory Processes. Journal of Computational and Applied Mathematics, 43, 3-18.
http://dx.doi.org/10.1016/0377-0427(92)90256-W - 2. Szabados, J. and Vertesi, P. (1990) Interpolation of Functions. World Scientific, Singapore.
- 3. Wang, X. (2011) The Approximation of Hermite Interpolation on the Weighted Mean Norm. Journal of Tianjin Normal University, 31, 7-12.
- 4. Xia, Y. and Xu, G.Q. (2010) The Approximation of Hermite Interpolation on the Weighted Mean Norm. Journal of Tianjin Normal University, 31, 6-10.
- 5. Xu, G.Q., Cui, R. and Wang, X. (2009) The Simultaneous Approximation of Quasi-Hermite Interpolation on the Weighted Mean Norm. International Journal of Wavelets, Multiresolution and Information Processing, 7, 825-837.
http://dx.doi.org/10.1142/S0219691309003276 - 6. Xie, T.F. and Zhou, S.P. (1998) Real Function Approximation Theory. Hangzhou University Press, Hangzhou.
- 7. Kingore, T. (1993) An Elementary Simultaneous Polynomials. Proceedings of the American Mathematical Society, 118, 529-536.
http://dx.doi.org/10.1090/S0002-9939-1993-1129881-X
上一篇:On the Location of Zeros of Po 下一篇:Computer Simulation of Transit
最新文章NEWS
- Auto-Bäcklund Transformation and Extended Tanh-Function Methods to Solve the Time-Dependent Coeffici
- A Third-Order Scheme for Numerical Fluxes to Guarantee Non-Negative Coefficients for Advection-Diffu
- Conjugate Effects of Radiation and Joule Heating on Magnetohydrodynamic Free Convection Flow along a
- An O(k<sup>2</sup>+kh<sup>2</sup>+h<sup>2</sup>) Accurate Two-le
- On the Location of Zeros of Polynomials
- Peristaltic Pumping of a Conducting Sisko Fluid through Porous Medium with Heat and Mass Transfer
- An Accurate Numerical Integrator for the Solution of Black Scholes Financial Model Equation
- Simulation of Time-Dependent Schrödinger Equation in the Position and Momentum Domains
推荐期刊Tui Jian
- Chinese Journal of Integrative Medicine
- Journal of Genetics and Genomics
- Journal of Bionic Engineering
- Pedosphere
- Chinese Journal of Structural Chemistry
- Nuclear Science and Techniques
- 《传媒》
- 《中学生报》教研周刊
热点文章HOT
- Asymptotic Solutions for the Fifth Order Critically Damped Nonlinear Systems in the Case for Small E
- Partial Fraction Decomposition by Repeated Synthetic Division
- Higher-Order Numerical Solution of Two-Dimensional Coupled Burgers’ Equations
- Group Method Analysis of MHD Mixed Convective Flow Past on a Moving Curved Surface with Suction
- Simple and Multi Linear Regression Model of Verbs in Quran
- Conjugate Effects of Radiation and Joule Heating on Magnetohydrodynamic Free Convection Flow along a
- Peristaltic Pumping of a Conducting Sisko Fluid through Porous Medium with Heat and Mass Transfer
- An O(k<sup>2</sup>+kh<sup>2</sup>+h<sup>2</sup>) Accurate Two-le
