Received 1 June 2015; accepted 10 July 2015; published 13 July 2015

ABSTRACT

The diabatic heating is calculated, using the thermodynamic equation in isobaric coordinates, of a heavy rainstorm that developed over Jeddah, Saudi Arabia on 25 November 2009. Throughout the period of study, the horizontal heat advection is the dominant term and the vertical advection term is opposed by the adiabatic one. The contribution of the local temperature term to the change in diabatic heating is relatively very minimal. The presence of the Red Sea and its adjacent mountains suggest that the diabatic heating in the lower atmosphere on that rainy day is primarily due to the latent heat released by convection. The dynamics of the studied case is also investigated in terms of isobaric Potential Vorticity (PV). The results show that the heating region coincides with the location of the low-level PV anomaly. Ertel’s Potential Vorticity (EPV) generation estimates imply that condensation supplies a large enough source of moisture to account for the presence of the low-level EPV anomaly. The low-level diabatic heating-produced PV assisted in amplifying the surface thermal wave early in the rainstorm development and in the upper-level wave during the later stages of the system’s growth.

Keywords:

Potential Vorticity, Diabatic Heating, Moisture Processes, Convection, Heavy Rainstorm, Saudi Arabia

1. Introduction

Diabatic heating is the essential force driving atmospheric circulation. The diabatic heating of the atmosphere consists of the release of latent heat, sensible heating and radiative heating as well as cooling. However, the understanding of diabatic heating has been hindered because atmospheric heating cannot be directly measured and must be estimated indirectly from other variables. Many investigations have examined the influence of moisture on the intensity of mature cyclones. However, an issue of considerable importance is how cyclone structure and propagation are altered by the presence of moisture throughout its phases of development. This issue was partly addressed theoretically by [1] who proposed, based on observations, that condensation takes place under slantwise neutral conditions. The resulting structure of two-dimensional, baroclinic waves with this constraint exhibited an intense updraft of a very small horizontal scale, but a nearly unchanged descent region. The characteristic strong and sloping updraft has been noticed in numerical simulations [2] and in observations [3] of intense cyclones. The full three-dimensional picture of the influence of condensation on the lifecycle of baroclinic waves is still incomplete. Indeed, too few studies have been conducted on the development of convection, and it remains an important issue to discuss.

Previous case studies have shown that diabatic potential vorticity (PV) maxima in the lower troposphere can influence on the evolution of extratropical cyclones [4] -[7] . In many cases, the diabatic PV maximum enhances the coupling and mutual interaction between the upper-tropospheric PV maximum and the surface potential temperature (θ) maximum, leading to a stronger feedback process and a more intense cyclone [6] [8] . However, in other cases, the diabatic PV maximum can hinder the interaction of the tropopause and surface waves [9] . Diabatically generated lower-tropospheric PV maxima can significantly influence the wind field in this layer of the atmosphere where there is a lot of moisture. This can significantly modify moisture transport and ultimately precipitation distribution through enhancement of the low-level jet [10] -[13] . Additionally, enhanced low-level jets can result in the transport of high-momentum air to the surface, resulting in damaging wind gusts in convective or non-convective situations.

Many studies attribute the PV concentration to the diabatic heating gradients that are present in the stratiform precipitation region of a mesoscale convective system [14] -[17] . This traditional view is supported by the fact that mesoscale convective vortices are consistently observed to develop in the stratiform component of mesoscale convective systems. However, the diabatic heating profiles presented by [18] [19] imply that the PV concentration may be derived from either convective or stratiform processes. When vertical gradients of diabatic heating act upon vorticity centers, they produce a concentration of PV substance [20] [21] in mid-levels and a dilution of PV substance above, resulting in approximate vertical stacking of positive and negative PV anomalies. The aim of this work is to study the relationship between diabatic processes and the generation of the low level-potential vorticity anomaly throughout the lifecycle of the mesoscale convective system (severe thunderstorm) that occurred over Jeddah, Saudi Arabia on 25 November 2009.

2. Theoretical Considerations

2.1. The Diabatic Heating

From elementary thermodynamic we find that

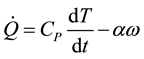(1)

where is the diabatic heating rate per unit mass, T the temperature, α the specific volume, C_p the

specific heat at constant pressure, and ω = dP/dt. Expanding dT/dt and rearranging the terms in Equation (1), the thermodynamic energy equation in isobaric coordinates per unit mass is given by

(2)

where V is the horizontal wind vector and Ñ the two-dimensional del operator on the isobaric surface. According

to Equation (2), 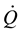can be estimated as a residual

(3)

Thus, diabatic heating changes are determined by quasi-horizontal temperature advection (V.ÑT), adiabatic temperature changes associated with work done on (ω > 0) or by (ω < 0) the air parcel on the environment during vertical displacements (−ωα/C_p), local temperature changes, (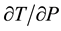), and vertical temperature advection

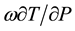(). The main processes that contribute to 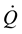are the release of latent heat due to condensation of water

vapour, turbulent flux and short-long wave radiations.

2.2. Estimation of Potential Vorticity

Potential vorticity fields were calculated from the available meteorological parameters, namely temperature and the horizontal wind components on constant pressure surface. In isobaric coordinates the potential vorticity was approximated by the product of the vertical components of absolute vorticity and potential temperature gradients as

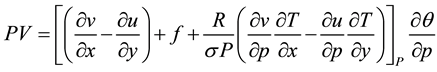(4)

where f is the coriolis parameter, q is the potential temperature u the wind in x-direction of the grid (W-E in principle) and v the wind in y-direction. Following [22] the dynamic tropopause is defined by the potential vorticity with P = 1.6 ´ 10⁻⁷ Kpa⁻¹∙s⁻¹ = 1.6 PVU, where, for convenience, the potential vorticity unit (PVU) is set as 10⁻⁷ Kpa⁻¹∙s⁻¹.

3. Data and Computation

3.1. Data

The data used in this study have been taken from the archives of the European Centre for Medium-Range Weather Forecasts (ECMWF; http://www.ecmwf.int/). They consist of the horizontal wind components (u- eastward, v-northward), the temperature (T) and the geopotential height (z) on regular latitude-longitude grid points (resolution 2.5˚ × 2.5˚) for the isobaric levels 1000, 850, 700, 500, 400, 300, 250, 200, 150 and 100 hPa. The data used are at 00:00, 06:00, 12:00 and 18:00 GMT during the period 23 to 26 November 2009. The study domain extends from 10˚W to 60˚E and from 10˚N to 60˚N.

3.2. Analytical Procedures

The diabatic heating is calculated using Equation (3) at 00:00, 06:00, 12:00 and 18:00 GMT. Therefore, time derivatives evaluated by centered finite difference spanning 12 hours provide a reasonable indication of the time variation of heating. Centered finite differences were used to compute horizontal derivatives and all vertical derivatives except those at 1000 and 100 hPa, where non-centered differences were employed. The inner domain used for calculating the terms of the thermodynamic Equation 3 extends from 37.5˚E to 47.5˚E and from 17.5˚N to 27.5˚N. Each term in the Equation (3) is diagnostically calculated. In the present study, the vertically inte-

grated diabatic heating term for different atmospheric levels has been determined. Therefore, the diabatic

heating rate is evaluated using a residual, by summing all the terms in the Equation (3). The tendency term is calculated as a centered finite differences scheme. The diabatic heating, evaluated in terms of the thermodynamic equation in isobaric coordinates, is affected by the evaluation of the vertical motion (ω). This motion is computed using the Q-vector representation of the quasi-geostrophic ω equation [23] , using the relaxation method [24] . All terms in Equation (3) are expressed as heating rates per unit mass and can be translated into daily heating by the following conversion, 1 W∙Kg⁻¹ = 86 K∙d⁻¹. Centered finite differences were also used to compute horizontal derivatives and all the vertical derivatives of the potential vorticity Equation (4) except those at 1000 and 100 hPa.

4. Results and Discussion

On 25 November 2009, heavy rainstorms hit Jeddah, Makkah and other regions in the western Saudi Arabia, as seen from the high-resolution (25 km × 25 km) Tropical Rainfall Measuring Mission satellite and observed rainfall merged product (not shown). The Jeddah station recorded 74.0 millimeters of rain in just four hours. This amount of rainfall in Jeddah is nearly twice the average for an entire year and the heaviest rainfall in Saudi Arabia in a decade. The dynamics of this 25 November 2009 heavy rainstorm case is studied through the winter depression that developed over the Mediterranean Sea for the period 00:00 GMT (03:00 local time) on 23 November to 12:00 GMT on 26 November 2009. Based on 1000 hPa and 700 hPa charts, the lifecycle of this studied case can be divided into two periods. The first period (growth) is from 00:00 GMT on 23 November to 12:00 GMT on 25 November while the second period (decay) is from 06:00 GMT on 26 November to 12:00 GMT on 27 November.

Geopotential height in meters (gpm) and temperature in ˚C on the 1000 hPa and 700 hPa charts at 00:00 and 12:00 GMT on each day of the period 23-26 November are shown in Figure 1 and Figure 2, respectively. At 00:00 GMT on 23 November, Figure 1(a) shows that the subtropical high pressure dominates over North Africa and the Mediterranean area; it also extends easterly to cover the north of Saudi Arabia and the East Mediterranean countries. The figure also illustrates that the Sudan low and its associated inverted v-shaped trough (Red Sea trough) oscillate northward to cover the east of Egypt and the entire Red Sea region. A clear thermal gradient associated with the northward oscillation of Red Sea trough extends zonally to cover the south of Saudi Arabia and the north of Sudan. During the next 12 hours (12:00 GMT on 23 November), the subtropical high weakens and moves eastward, while the Red Sea trough propagates slowly northward and the Sudan low deepens to 80 gpm (Figure 1(b)). The system first appears as an extension of the traveling depression, east of the Mediterranean at 00:00 GMT on 23 November (Figure 2). A cut-off low is formed at 12:00 GMT on 23 November and a well-defined cyclonic depression becomes clear over Egypt (Figure 2(b)). At 00:00 GMT on 23 November, a thermal gradient lies along the northeast of Saudi Arabia; this baroclinic zone leads to the formation of an upper level cut-off low. At 00:00 GMT on 24 November a strong development occurs at the surface and in the upper atmosphere, where the Sudan low at the surface and its associated Red Sea trough moves northward to cover the north of the East Mediterranean, Egypt and Saudi Arabia. The center of the Sudan low is present over the Red Sea (15˚N and 37.5˚E), while the geoptential height at the center reaches 100 gpm. In the upper atmosphere (700 hPa), the cut-off low deepens and moves slowly eastward to reaching just north of Egypt; the geopotential height at the center reaches 3100 gpm (Figure 2(c)).

During the next 12 hours (12:00 GMT on 24 November), the inverted v-shaped trough associated with the Sudan low oscillates northward and in the upper atmosphere (700 hPa), the cut-off low also moves eastward to reach just northeast of Egypt. During the period 18:00 GMT on 24 November to 12:00 GMT on 25 November (the rainy period), a strong interaction occurs between the inverted v-shaped troughs extending from the tropical region and from mid-latitude region. The two depressions merge to form a single system. The most interesting features are the strong northward warm advection from the tropical region associated with the air flow around the Sudan low, and the strong southward cold advection. The interaction between these two air masses causes a great deal of instability over the East Mediterranean and the west of Saudi Arabia.

After 12:00 GMT on 25 November, the inverted v-shaped trough of the Sudan low moves south-westward while the upper air trough retreats westward where the associated cut-off low is centered over the northwest of Egypt, and the interaction between the two troughs vanishes. During the next day (26 November), the depression starts to weaken and its central pressure increases gradually. On the other hand, the subtropical high pressure over North Africa and the western Mediterranean is extended with a major ridge that joins the Siberian high on 27 November. In other words, no more cold advection is permitted to the system. While the Siberian high pressure propagates westward, the horizontal extension of the system decreases and moves slowly eastward. It becomes a stationary vortex rotating above the northeast of the Mediterranean (Figure 2(g), Figure 2(h)). Finally the system drifts slowly north-eastward and leaves the area by 28 November (not shown)

4.1. Spatial Distribution of Diabatic Heating

The results of the diabatic heating rate in 8 time steps starting from 06:00 GMT on 24 November to 00:00 GMT on 26 November 2009 are presented. As the interest is to examine the time variations of the diabatic heating for the studied case, Figure 3 illustrates the spatial distribution of the diabatic heating rate at 1000 hPa during the life cycle of the studied system. The daily pattern of diabatic heating is shown in Figure 3, which indicates that at the west of the 1000 hPa trough (approximately west of the Red Sea), a cold sector exists with diabatic cooling; while to the east of the trough, diabatic heating prevails. By comparing the horizontal distribution of the

1000 hPa diabatic heating in Figure 3 with geopotential height and temperature at 1000 and 850 hPa in Figure 1 and Figure 4 respectively, it is noted that the western part of the trough (which is the area of downward motion),

there is a region of diabatic cooling, and at the eastern side of the trough (the area of upward vertical motion), there is a dominant region of diabatic heating. In other words, the diabatic heating behaves like warm advection, and the diabatic cooling behaves like cold advection. Therefore, diabatic heating/cooling in the vicinity of developing convection is usually associated with rising/sinking motions, respectively. Strictly speaking, a relative maximum in diabatic heating is associated with rising motion while a relative minimum in diabatic heating is associated with sinking motion.

By looking at the time variation of heating and cooling over the inner domain, which is used for the present calculation, two main features of the horizontal distribution of heating rates at 06:00 GMT on 24 November 2009 can be seen (Figure 3). One feature that stands out clearly is a cooling maximum off the west coast of the Red Sea over Egypt and north of Sudan (the maximum cooling is 0.25 K/6h). This maximum cooling appears to be related to the presence and penetration of the intense westerly cold air. The maximum cooling tends to decrease southward over the south-western parts of the Red Sea, suggesting that the source of cooling is due to the advection of cold arctic air across most of the Mediterranean Sea. Another notable feature is the temporal variation of the heating pattern over northern Saudi Arabia. Actually, the temporal variations of these two features are significant. It was detected that the cooling, found over the north-western parts of the Red Sea at 12:00 GMT on 24 November 2009, moved slowly southward between 18:00 GMT on 24 November to 00:00 GMT on 25 November. It was eventually weakened, before the center of the heating moved southward and was also weakened. The cooling over the eastern parts of the Red Sea moved eastward with intensification over northern Sudan during the period 06:00-12:00 GMT on 25 November. At the same time, a heating area redeveloped over north- eastern Saudi Arabia and then moved north-eastward. The maximum heating (occurring at 00:00 GMT on 25 November) was found to be associated with the maximum deepening of the storm system. The movement of the heating or cooling pattern is strongly associated with the movement of the storm. Finally, during the last two time steps (18:00 GMT on 25 November-00:00 on 26 November), the central cooling area over north-eastern Sudan moved slowly south-eastward and eventually weakened.

4.2. Time-Height Variations of Diabatic Heating

The estimation of the atmospheric diabatic heating in terms of the isobaric thermodynamic method allows the individual contribution of each effect to be examined [25] . Nevertheless, the utilization of the thermodynamic equation in isobaric coordinates provides a way to visualize how the diabatic heating is balanced by the horizontal advection of sensible heat and adiabatic heating due to vertical motion. The inner domain used for calculating the terms of the thermodynamic Equation 3 extends from 37.5˚E to 47.5˚E and from 17.5˚N to 27.5˚N.

The vertical transport of the diabatic heating through time-pressure cross-sections is shown in Figure 5. Figure 5(b) shows that the contributions of the local temperature term to the diabatic heating changes are relatively very minimal. This illustrates that there is an increase in temperature during the first four time steps except at the layer 1000 - 700 hPa of 06:00 and 12:00 GMT on 24 November and also above 150 hPa. On the rainy days (18:00 GMT on 24 November to 06:00 on 25 November), there is a local increase in temperature from the surface up to 700 hPa, while a local decrease of temperature occurs above 300 hPa. During the last two time steps, there is a local decrease in temperature from 300 hPa. Horizontal warm advection occurs at all levels during the period of study. It is evident that the largest contribution of the horizontal warm advection of temperature exists between 250 - 150 hPa at 18:00 GMT on 24 November and between 500 - 200 hPa during the last three time steps.

In the vertically averaged sense, the adiabatic term (−ωα/C_P) and vertical advection (ωϑT/ϑP) work in opposite senses, which imply that these two terms numerically cancel each other out when viewed in the time-pressure plane. However, these two terms do not balance each other exactly. Figure 5(d) and Figure 5(e) show that the contribution of the vertical temperature advection (ωϑT/ϑP) and the diabatic temperature term are opposite to each other. In other words, the areas of heating in Figure 5(d) coincide with the areas of cooling in Figure 5(e) and vice versa, which means that there is a strong negative correlation between the patterns of the adiabatic and vertical temperature terms. Figure 5(d) shows that ωϑT/ϑP tends to increase the temperature throughout the period of study. The maximum heat contribution of this term occurs at 12:00 and 18:00 GMT on 24 November, and 12:00 GMT on 25 November between 400 and 200 hPa. Figure 5(e) shows that adiabatic term (−ωα/C_P) tends to decrease the temperature throughout the period of study. The maximum cool contribution of this term occurs at 06:00 and 18:00 GMT on 24 November, and 12:00 GMT on 25 November between 500 and 200 hPa.

Figure 5(a) illustrates the diabatic heating as the sum of the four terms on the right hand side of Equation (3).

The outstanding features here are the heating at all levels during the period of study. The existence of the Red Sea and its adjacent mountains supports the suggestion that the diabatic heating in the lower atmosphere is primarily due to latent heat being released from the developed convection.

4.3. Generation of the Low-Level PV Anomaly

Usually, intense low-level Ertel’s potential vorticity (EPV) anomalies have been observed in cyclone cases [26] [27] . In their cases, the air within the low-level EPV anomaly was not of stratospheric origin and the EPV anomalies were probably generated by condensation. Figure 6 illustrates the location and the development of the low-level EPV anomaly in association with the studied case, while Figure 7 shows the relative humidity (RH) pattern for the period from 06:00 GMT on 24 November to 00:00 GMT on 26 November. Generally, the regions of low-level EPV anomaly are associated with regions of high values of RH, which reach about 90%, indicating that the air within the central region of the EPV anomaly is nearly saturated.

Figure 8 illustrates the vertical velocity at 850 hPa for the period of study. It shows the movement of the centers for upward and downward velocities with the movement of the storm during its development. The regions

of low-level EPV anomaly (Figure 6) are associated with the areas of negative vertical motion (Figure 8); this is verified throughout the period of study. Figure 6, Figure 8 and the above discussion indicate that strong diabatic processes occur in the vicinity of the low EPV anomaly.

For a more in-depth understanding, the EPV generation rate from latent heat release is estimated. Following [4] , the method uses the solution to the balanced ω-equation, with the latent heat release allowed in regions of saturated ascent (incorporated as locally reduced static stability), to calculate and then EPV generation from:

(5)

where the subscript LH refers only to condensational heating. The regions of reduced static stability are initially unknown and are found through iteration during the ω-equation inversion. The horizontal gradients of heating in this calculation were included, which can be significant in frontal zones. In addition, the non-conservative generation term is free to feedback on the flow tendency and vertical velocity. Figure 9 displays the EPV generation rates at 850 hPa obtained by the above method. It shows that at 06:00 on 24 November, there was a cell of EPV tendency at 30˚N, 39˚E with a central value of 0.8 PVU/12h, at 12:00 on 24 November. The EPV tendency cell moved eastward to 30˚N, 40˚E with a central value of 0.5 PVU/12h. In the following 6 hours, the EPV tendency cell occupied a larger area and extended southward to reach the south of Saudi Arabia. On 25 November 2009 (00:00 GMT), the cell of the EPV tendency became closer over the middle of the west of Saudi Arabia, its central value was more than 0.4 PVU/12h, at 21˚ N, 42˚ E. At 00:06 GMT on 25 November, the cell of the EPV tendency moved north-eastward and weakened over the west and middle of Saudi Arabia. Its center moved to the north of the Arabian Gulf and had a value 0.5 PVU/12h. In the following three time steps, the cell of the EPV rate stayed over the north of the Arabian Gulf (northeast of Saudi Arabia) in association with the movement of the studied system.

The results of the above discussion indicate that the heating region coincides with the location of the low-level PV anomaly and the EPV generation estimates, and implies that condensation provides a large enough source to account for the presence of the low-level EPV anomaly. The condensation produces a low-level EPV anomaly that adds directly to the low-level PV anomaly, which in turn is strongly influenced by moisture processes.

The low-level diabatically produced PV assists in amplifying the surface thermal wave early in the development of the studied system and in the upper-level wave during the later growth stages. A further application of the quantitative diagnostics discussed in this work is recommended, continuing into the dynamics of synoptic and large-scale systems. This promises to provide a common ground through which observational, numerical and theoretical work may be easily compared.

5. Conclusions

The aim of this paper has been to study the relationship between the diabatic processes and the generation of the low-level potential vorticity anomaly throughout the lifecycle of a rainstorm, which developed in Saudia Arabia on 25 November 2009 when Jeddah, Makkah and other regions received heavy rainfall. Calculations of the diabatic heating have been made using the thermodynamic equation in isobaric coordinates. The horizontal heat advection is the dominant term during the lifecycle of the system. This means that the diabatic heating is strongly associated with the warm air advected into the region. The analyses of the time-height variations of the terms illustrate that the contribution of vertical temperature advection and the adiabatic term are opposite to each other, which means that there is a strong negative correlation between the patterns of the adiabatic and the vertical temperature advection terms. The contributions of the term of local temperature changes to the diabatic heating rates are very small with respect to all the other terms. The presence of the Red Sea and its adjacent mountains supports the suggestion that the diabatic heating in the lower atmosphere is primarily due to the latent heat release on the rainy day.

The dynamics of the rainstorm system have been investigated also in terms of isobaric potential vorticity. On the whole, this approach seems to identify the same features for rainstorm initiation: an isobaric PV anomaly at the lower levels with a low-level baroclinic zone (with a shallow frontal system). The PV analysis identified possible effects at low levels in the central Red Sea (where the positive lower PV anomaly resulted from the

condensation of water vapor), an area where the diabatic processes appear to play an important role in convection development. It is also found that the heating region coincides with the location of the low-level PV anomaly and the EPV generation estimates, which implies that condensation provides a large enough source to account for the presence of the low-level EPV anomaly. The condensation produces a low-level EPV anomaly that adds directly to the low-level PV anomaly, which in turn is strongly influenced by moisture processes. The low- level diabatically produced PV assisted in amplifying the surface thermal wave early in the convection development and in the upper-level wave during the later stages of the system’s growth.

Acknowledgements

The authors would like to acknowledge the support of the King Abdulaziz University (KAU) and the Presidency of Meteorology and Environment in Saudi Arabia (PME). The NCEP data are obtained from their website.

Cite this paper

H.Abdel-Basset,A. K.AL-Khalaf,A.Albar, (2015) Diabatic Processes and the Generation of the Low-Level Potential Vorticity Anomaly of a Rainstorm in Saudi Arabia. Atmospheric and Climate Sciences,05,275-291. doi: 10.4236/acs.2015.53021

References