Received 1 June 2015; accepted 6 October 2015; published 9 October 2015

ABSTRACT

An analysis of the kinetic energy budget is made for a tropical cyclone. Horizontal flux convergence constitutes a major energy source. Generation of kinetic energy via cross-contour flow is a persistent sink throughout the pre-storm and growth periods. Dissipation of kinetic energy from subgrid to grid scales is an important source during the pre-storm and growth periods; it acts as the major sink of energy during the decay period. The major contribution to kinetic energy comes from a persistent upper tropospheric jet stream activity throughout the period of the cyclone development. Unlike midlatitude cyclones, a considerable quantity of kinetic energy appears between 850 - 500 hPa layers especially during the growth period. While the behavior of the values of horizontal divergence by nondivergent wind closely resemble to those of total horizontal divergence term, neglecting the divergent part of the wind would clearly lead to a considerable error in the calculation of total horizontal divergence. The mean error in approximation of total horizontal divergence by the nondivergent part during the life cycle of our cyclone is about 36%.

Keywords:

Kinetic Energy Budget, Tropical Cyclone, Divergent Wind, Rotational Wind, Dissipation of Energy, Jet Stream, Generation of Energy

1. Introduction

Tropical cyclone landfall engages numerous important issues including structure/change in intensity and track turning when it moves towards coastal area, sustention and decay over land, storm surge, wind strength and rainfall. The land falling tropical cyclone rainfall is one of the majority complex issues. When a tropical cyclone approaches the coastal area, interaction between ocean, atmosphere and land topography should be considered. The greater part of the severe disasters or catastrophes were often caused by heavy rainfall of a land falling tropical cyclone which could result in flash flooding, reservoir collapses and debris flow to threaten the loss of lives and properties. Extreme weather events and disasters from landfalling tropical cyclone occurred in both Pacific and Atlantic coastal regions frequently, especially in recent years, such as super typhoons [1] . A number of the damages were caused by heavy precipitation from those typhoons and hurricanes. Accurate forecasts and warnings on tropical cyclone rainfall in this connection will play an important role for disaster avoidance and preparedness.

Many studies are applied to convectively unstable synoptic situations [2] - [7] . Synoptic-scale kinetic energy analysis has shown convective storm environments to be regions of intense energy transformations and transports [8] - [10] . Widespread convection is thought to be a source of synoptic-scale kinetic energy [11] due to transfer of unresolvable (subgrid) to resolvable (grid) scales of motion [12] - [14] . Sources and sinks of kinetic energy within the mesoscale storm environment appear to be more intense than those at the larger scales [15] - [21] . The coupling of convection to synoptic-scale processes is explored [22] . The bulk upscale influences of convection in baroclinic cyclones obviously force the downstream synoptic scale and instant mesoscale environment. This includes: enhanced differential cyclonic vorticity advection ahead of weak upstream troughs resulting from convection-generated enhanced downstream ridging and jet development with landfalling and recurving tropical cyclones [23] [24] ; vorticity buildup and merger in vortical hot convective towers throughout initial tropical cyclogenesis [25] ; and mesoscale ridging in the upper troposphere ahead of convection linked with mesoscale convective vortices [26] .

A different approach for describing kinetic energy balance is to regard as the relative contributions of the divergent and rotational wind components. Using summertime data of Northern Hemispheric, the ratio of divergent kinetic energy to the total amount is approximately 0.10 to be found [27] . In other words, the dominant component of 200 hPa tropical flow is the rotational wind [28] - [33] . While the divergent wind was small in magnitude, it assumed vital importance in the generation and transport of kinetic energy within a midlatitude cyclone [34] . Likewise kinetic energy of the Arabian Sea monsoon was observed to increase via interactions between the divergent and rotational wind components [35] . Conversely, a lot of the cross contour generation of kinetic energy in some cyclones has been attributed to the rotational wind [36] [37] . The purpose of the present study is to discuss and analyze the kinetic energy budget of a developing tropical cyclone over a limited area during 14 to 25 October 2008. Also, to examine the relative contributions of the divergent and nondivergent wind components to the kinetic energy budget.

2. Theoretical Consideration

The Kinetic Energy Equation

In pressure coordinates, the kinetic energy equation given by [13] in an atmospheric column is

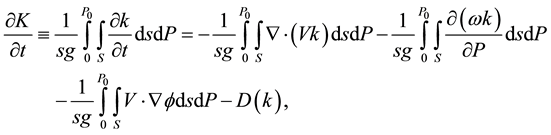(1)

where S is the area of computational domain, g is the acceleration due to the gravity and P₀ is the surface pressure. On the right-hand side of Equation (1), the first and second terms are the horizontal and vertical flux divergence of kinetic energy, the third term is the generation of kinetic energy due to the cross-contour flow and the last term D (k), commonly called the “dissipation” term.

To examine contributions of the divergent and rotational winds to the total kinetic energy balance, these components must be introduced into Equation (1). This can be done by following the procedure of [34] .

Helmholtz’s theorem states that horizontal wind can be expressed as the sum of the divergent (V_D) and non-divergent (or rotational) components (V_R), i.e.,

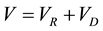(2)

The kinetic energy per unit mass can be expressed as

(3)

where

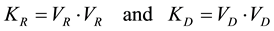(4)

Using Equation (2), we may write the integrands of the first and third terms on the right-hand side of (1) as

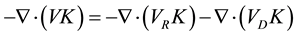(5)

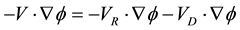(6)

Equation (5) shows that the horizontal flux convergence of kinetic energy is caused by the horizontal transport of non-divergent and divergent winds. For sake of convenience we associate 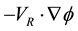and 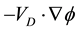with the generation of kinetic energy due to barotropic and baroclinic processes, respectively [27] [38] . The barotropic term integrates to zero in a closed domain [27] , but not in an open domain as considered here. Using (5) and (6), we can rewrite (1) as

(7)

We shall pay particular attention to the contribution of V_R and V_D to kinetic energy in Equation (3), to the horizontal flux convergence 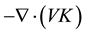of kinetic energy in Equation (5), and to the generation of kinetic energy in Equation (6).

3. Data and Computation

3.1. Input Data

The data used in this study have been taken from the archives of the European Center for Medium-Range Weather Forecasts (ECMWF). It consists of the horizontal wind components (u―eastward, v―northward), the temperature (T) and the geopotential height (Z) on regular latitude-longitude grid points resolution of 2.5˚ × 2.5˚. The used data is only at 1200 GMT during the period 14 to 25 October 2008 for isobaric levels 1000, 850, 700, 500, 400, 300, 250, 200, 150 and 100 hPa. The domain of the study extends from 25˚ to 65˚ and from 0˚ to 40˚. The 1200 GMT was used for the present study. The inner domain which is used for the present case of study in calculations of kinetic energy budget is shown in Figure 1 and Figure 2.

3.2. Analytical Procedures

The vertical wind component in the P-coordinate system, namely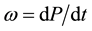, is estimated using the kinematic method. However, due to errors in horizontal divergence estimates, accumulation of error in occurs away from the bottom of the atmosphere. To remove this bias a pressure-weighted correction for w was adopted following [39] . This technique was employed to calculate grid point values of w at all standard isobaric levels and at the midpoint of each sub layer. At the bottom and the top of the atmosphere w was initially set to zero.

An advanced technique for obtaining divergent and non-divergent winds (V_D and V_R) is the solution of poisson equations for stream function and velocity potential using the relaxation method [40] . The energy variables are calculated at 1200 GMT. Therefore, time derivatives evaluated by central differences spanning of 48h give a reasonable indication of the time variation of kinetic energy. Centered finite differences were used to compute horizontal derivatives and all vertical derivatives except those at the 1000 and 100 hPa, where non-centered differences were employed. For each of wind analysis at 1000 hPa, energy variables at this level are obtained by linear extrapolation. Finally, the dissipation term is evaluated as a residual in Equation (1) [41] . [42] warns of the risk in attaching physical significance to the sign or magnitude of residual terms, but concedes that application of the residual technique may be meaningful in data-rich areas.

4. Synoptic Discussion

A common case of tropical cyclogenesis over the Indian Ocean is considered in the present study. Its period continued from 14 to 25 October 2008. Figure 3(a) illustrates the track of the tropical cyclone during the period 14 to 25 October 2008 while Figure 3(b) shows pressure and temperature values at the center of the tropical cyclone during this period. Based on the surface charts, changes in central pressure and charts of 1000 and 700

hPa the life cycle of this cyclone can be divided as following: Pre-storm period: 14-16 October, Growth period: 17-21 October , Decay period: 22-25 October. 1000 and 700 hPa charts at 1200 GMT on each day are shown in Figure 1 and Figure 4 and Figure 5, respectively. 1000 and 700 hPa charts contain contours of height with 10 meter increment and isotherms with 2oc increment.

The cyclone of special interest first appeared as an extension of the equatorial trough south of India at 14 and 15 October, a cut-off low formed at 16 October and a well-defined cyclonic depression become clear over south west of India (Figure 4). The 700 hPa trough (Figure 1) associated with the cyclone is well southwest of India by 16 October, a cut of low at 700 hPa was centered over Indian Ocean at (6˚N, 65˚E), Figure 1. At 17 October the trough extended westward and the surface storm undergoes strong intensification. A closed 700 hPa contour developed and moved west at 18 October. The maximum development occurs at 19 October where the pressure at center of the surface low decreased to 999 hPa, a drop in the contours of 1000 and 700 hPa levels taken place in conjunction with the deepening surface cyclone.

By 20 October the cyclone moved slowly northwest ward and its center pressure at the surface increased one hPa. During the next 24 hours the cyclone also moved northwest ward to reach the coast of the southeast of Yemen. By 21 October the slow moving ridge of Siberian high began to move northward. While the Siberian high moved (shifted) northward the horizontal extension of the cyclone increases and moved slowly westward. The most pronounced feature at 21 October is the existence of a strong thermal gradient north of our cyclone and associated with the south coast of Arabian Peninsula at 1000 hPa. By 22 October the cyclone moved westward to become over Gulf of Aden, Yemen and north of Somalia associated with a developing thermal trough forming highly baroclinic zone. By 23 October while the Siberian high pressure propagate southward the horizontal extension of the cyclone decreases and moved slowly eastward (Figure 5(b)). While the pressure at the center of the surface low increased to 1005 hPa. Continuous rainfall over Yemen and southwest of Saudi Arabia occurs at

22, 23 October. At 24 October the extension of the surface low propagate northward over the west of Saudi Arabia and Red sea. This northward oscillation of this trough coincide with the entrance of upper air trough from the Mediterranean, this situation causes strong instability over Red sea and most regions of west Saudi Arabia. Finally, the cyclone was drifted slowly northeast ward (cover east of Sudan) and weaking.

5. Analysis of Total Kinetic Energy Budget

5.1. Kinetic Energy Time Development

The energy budget in terms of the Eulerian kinetic energy Equation (1) is evaluated in a domain which encloses our cyclone during its life cycle. The area-mean energy variables, integrated from 1000 100 hPa at 1200 GMT are shown in Table 1. Note that the vertical flux divergence was integrated to zero because of the solid boundary condition on w, therefore, is not presented in Table 1.

5.1.1. Pre-Storm Period

Table 1 shows that the generation of kinetic energy term, , is negative which indicate on average that the cross contour flow is down gradient in the vicinity of the cyclone. The gradual strengthing of the cyclone (Figure 1) explain the monotonic increase in kinetic energy and also the local variation of kinetic energy. Horizontal flux convergence contributes significantly to the energy budget of our cyclone. Dissipation of kinetic energy from subgrid to grid scales is an important source during this period.

5.1.2. Growth Stage

The kinetic energy increases during the growth period and reaches its maximum value at 19 October. The local variation of kinetic energy, ¶K/¶t, is positive throughout the first two days of this period and become negative during the later portion when the cyclone tends to decay. Generation of kinetic energy is a prominent sink. The magnitude of this term is evidence of widespread and persistent imbalance in the mass and wind fields. The negative values of the generation term on average indicate that the cross contour flow is down gradient in the vicinity of the cyclone. The major source of kinetic energy for the cyclone is the dissipation term during the first

two days and the horizontal flux convergence during the last two days in this stage. As it is expected, the dissipation D (K) is greatest when the storm is most intensive. An overview of the kinetic energy budget is obtained by comparing the external source or sink and the internal source or sink [34] . Table 1 shows clearly that external source dominates during the last three days in the growth stage.

5.1.3. Decay Stage

The deterioration of the storm system is demonstrated by a steady decrease in kinetic energy during the first two days in this stage. This occurs according to the fact that horizontal transport continues to represent a major energy source, so this provides a permanent source of energy to the region. Generation of kinetic energy represent another source of energy in this period only, and the dissipation combines to yield an internal sink that exceeds the external source of kinetic energy.

5.2. Vertical Distribution of Time Mean-Kinetic Energy

The time-mean kinetic energy budget for our cyclone, at individual pressure levels, is shown in Table 2. The major contribution to the kinetic energy comes from a persistent upper tropospheric jet stream activity throughout the period of our cyclone. The most of this energy occurred above 250 hPa in association with the strong jet stream. The local derivative term indicates that average kinetic energy increased slightly with time at the levels above 850 hPa except at the upper level (100 hPa). The term, , indicates the vertical transport of kinetic energy, positive values indicating downward transport. Downward transport of kinetic energy is found in the layer (500 - 150 hPa). In the lower layer (1000 - 700 hPa) the vertical flux is negative which indicate that the transport of kinetic energy aloft by the upward motion dominate throughout the period. This vertical transport acts as a source of kinetic energy to the middle and upper troposphere.

Positive dissipation term, is suggesting a transfer of energy from subgrid to grid scales of motion as a source of energy at all levels except at 300, 250, 150 and 100 hPa. Positive values of this term have been reported by numerous other investigators [17] [43] [44] . A considerable amount of energy is transported out the area by horizontal flux convergence below 300 hPa. Above 400 hPa the horizontal flux convergence serves as a major source at all levels throughout the period and reaches its maximum values near the jet level and produce a mean value for in the order 1.29 w∙m⁻².

The generation of kinetic energy, , is negative at the most levels, which indicate that this term is a prominent sink in our case. The vertical profile of demonstrate that the maximum adiabatic destruction of kinetic energy is in the 700 - 400 hPa layer. The life cycle vertical average of is 0.41 w∙m⁻². Comparing both external source or sink and the internal source or sink we found that the external source dominates at all levels above 400 hPa.

5.3. Time-Height Variations of Budget Quantities

Energetic processes in relation to the cyclogenesis region need further examination and are analyzed by means of time-height cross sections as represented in Figure 6. The major feature of the cyclogenesis region is the field of kinetic energy due to the persistence of the upper jet stream between 250 - 150 hPa, and also due to maximum development during the growth period of our tropical cyclone between the layer 850 - 400 hPa.

Systematic changes, related to the life cycle of our case occur in the flux convergence term. There are positive values of horizontal flux convergence in upper half of the atmosphere. The maximum of this values (the maximum import of kinetic energy out of the region) near 150 hPa at 20 and 21 October. So, the horizontal flux convergence acts as a major source of energy at the upper levels during the growth and decay periods of our cyclone. This term acts as a sink of energy at all levels below 400 hPa throughout the life cycle of the cyclone except at 24 and 25 October. A transport of kinetic energy from the lower layer to the layer 700 - 400 hPa by vertical flux convergence occurs during pre-storm and growth periods. The pattern of this term is very variable where the most striking feature is the transport of energy downward from the layer between 700 - 300 hPa to the lower layer during the growth stage and from 700 - 200 hPa during the decay stage.

The life cycle of our case study is also well described through generation term −V×Ñf. In the pre-storm and growth stages a major energy sink is the intense conversion of kinetic to potential energy by the generation term

which reaches its maximum negative value at 19 October and becomes positive during the decay period. The maximum generation of kinetic energy appears above 400 hPa.

Transfer of kinetic energy from subgrid to larger scales of motion generally is the pronounced feature in our cyclone. Enhanced transfer from subgrid to grid scales of motion is prominent in the middle and upper troposphere and in the lower stratosphere during the growth stage. This term becomes negative and so dissipative losses are now quite prominent during the decay period.

5.4. Contribution of Divergent and Non-Divergent Wind Components to the Kinetic Energy Budget

5.4.1. Kinetic Energy

In their global study, [27] showed that the kinetic energy of the divergent wind K_D is very small compared to that of the nondivergent wind K_R. However, [45] noted that K_D may be significant in severe storms. Table 3 shows the contribution of the divergent and non-divergent wind to the kinetic energy and the ratios K_R/K, K_D/K and V_R×V_D/K for 24 h intervals during the evolution of the cyclone. Values of K, K_R and K_D all vary in the same direction while K_R has the major contribution to K. The dot product of the nondivergent and divergent winds V_R×V_D integrates to zero on the glob, but not necessarily in a limited domain. In our case of study term V_R×V_D is smaller than K_D. Values of V_R×V_D are generally smaller than those of K_D especially in the lower troposphere. The error in approximating K by K_R ranges from 4.5% to 6.6% and the average error during the period of cyclone is only about 5.5%. Tim-mean averages of the components of kinetic energies K, K_R, K_D and V_R×V_D and their ratios are expressed in Table 3.

5.4.2. Horizontal Flux Convergence of Kinetic Energy

The horizontal flux convergence of kinetic energy is regarded as an external energy source and represents the net flow into or out of an open system. The total flux convergence of kinetic energy, −Ñ∙Vk, may be splited into two parts, one due to the nondivergent wind −Ñ∙V_Rk and the other to the divergent wind −Ñ∙V_Dk. These quanti-

ties at different times in the life cycle of the cyclone are shown in Figure 8(a).

During the pre-storm period −Ñ∙V_Rk is negative and increases steady as −Ñ∙Vk during the growth period and becomes positive during the decay period. The horizontal flux convergence by the divergent wind is positive during the pre-storm and growth period while it negative during the decay period. While the behavior of the values of −Ñ∙V_Rk closely resemble to those of −Ñ∙Vk, neglecting the divergent part of the wind in our case of study would clearly lead to a considerable error in the calculation of −Ñ∙Vk. The mean error in approximation of −Ñ∙Vk by −Ñ∙V_Rk during the life cycle of our cyclone is about 36 %.

Figure 7(a) shows the horizontal flux convergence terms with pressure. The values of −Ñ×V_Rk is negative and greater than the negative values of −Ñ×V_Dk below 400 hPa, so the rotational and divergent winds exports energy below 400 hPa throughout the period of our cyclone. Above 300 hPa the values of −Ñ×V_Rk and −Ñ×V_Dk becomes positive and −Ñ×V_Rk is much greater than −Ñ×V_Dk. Figure 7(a) shows that the maximum import of energy occurs within the 250 - 150 hPa layer.

5.4.3. Generation of Kinetic Energy

The generation of kinetic energy by total wind (−V×Ñf), rotational wind (−V_R×Ñf) and the divergent wind (−V_D×Ñf) at different times of our case study are shown in Figure 8(b). The barotropic contribution −V_R×Ñf is almost negative except at the decay period. This may explain that nondivergent wind blows toward higher pressure most of the time except at the decay stage where the cross-contour flow to divergent wind is predominantly toward lower pressure. The maximum negative values of −V_R×Ñf occurs during the growth stage. The baroclinic contribution −V_D×Ñf acts as a sink of energy during the pre-storm and growth period while it acts as a source of energy during the decay period, the magnitude of this term is very small compared to −V_R×Ñf. The values of −V_R×Ñf are closely resemble to those of −V×Ñf, so, the average error in approximating −V_R×Ñf by −V×Ñf during the life cycle of the cyclone is very small.

Generation of kinetic energy is shown with the vertical pressure in Figure 7(b). Generation due to barotropic processes predominates at all levels below 300 hPa and on the other hand generation due to baroclinic processes is negative below 400 hPa and positive above 300 hPa. It can be conclude that generation of kinetic energy by barotropic component is the major source at all levels below 300 hPa. On the other hand the baroclinic component of generation is an energy sink below 400 hPa.

6. Concluding Remarks

This paper has described the kinetic energy budget and the relative contributions of divergent and rotational wind components to the kinetic energy balance during the period of a tropical cyclone. Generation of kinetic energy term acts as an energy sink throughout the pre-storm and growth periods, which indicate on average that the cross contour flow is down gradient in the vicinity of cyclone during these two periods. This term acts as energy sink during the decay period. Dissipation of kinetic energy from subgrid to grid scales is an important

source during the pre-storm and growth periods; it acts as the major sink of energy during the decay period. The horizontal flux convergence behaves as major source of energy during cyclone life cycle. The major contribution to kinetic energy comes from a persistent upper tropospheric jet stream activity throughout the period of the cyclone development. Unlike midlatitude cyclone a considerable quantity of kinetic energy appears at the layer between 850 - 500 hPa especially during the growth period. While the behavior of the values of −Ñ×V_Rk closely resemble to those of −Ñ×Vk, neglecting the divergent part of the wind in our case of study would clearly lead to a considerable errors in the calculation of −Ñ×Vk. The mean error in approximation of −Ñ×Vk by −Ñ×V_Rk during the life cycle of our cyclone is about 36%. Generation of kinetic energy by barotropic component is a source at all levels below 300 hPa, while the baroclinic component of generation is an energy sink below 400 hPa.

Cite this paper

HeshmatAbdel-Basset Mohamed,Mahmoud AhmedHusin,Hosny MohamedHasanen, (2015) Kinetic Energy Budget of a Tropical Cyclone. Atmospheric and Climate Sciences,05,394-407. doi: 10.4236/acs.2015.54031

References