欢迎来到期刊吧-专注期刊发表！
关于我们联系我们发表流程付款方式医学sci转让留言板
您的位置： 首页 > 国外期刊 > Atmospheric and Climate Sciences

Analysis of Rain Variability Using the Daily and Monthly Concentration Indexes in Southeastern Brazi

Vol.07No.02(2017), Article ID:74841,15 pages
10.4236/acs.2017.72013

Jonas T. Nery1, Ana Claudia Carfan1, Javier Martin-Vide2

1Department of Geography, UNESP, Ourinhos, Brazil

2Climatology Group, University of Barcelona, Barcelona, Spain

Copyright © 2017 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

Received: January 16, 2017; Accepted: March 19, 2017; Published: March 22, 2017

ABSTRACT

Daily and monthly rainfall was analyzed by the Concentration Index (CI) of [1] and the Annual Precipitation Concentration Index (PCI) of [2] in southeastern Brazil. About 120 rainfall stations were used in the period from 1976 to 2010. Data were obtained from the National Water Agency (ANA). These data were selected by observing their spatial and temporal distribution in the study area. In general, the Concentration Index and the Precipitation Concentration Index were consistent for the study of rainfall variability in the study area. High percentages of annual rainfall concentration in a few very rainy days can increase the risk of flooding and soil instability. In this work, a survey of the spatial and temporal patterns of daily and monthly rainfall concentration in southeast Brazil was conducted. The results showed a relatively homogeneous temporal distribution of daily rainfall in the study area. In addition, the Mann-Kendall test showed a clear trend towards a seasonal rainfall distribution.

Keywords:

Concentration Indices, Variability, Rain, Southeast, Brazil

1. Introduction

The climates of Brazil are highly controlled by factors such as latitude, altitude, oceanic influence, and dynamical systems from the extreme south of South America, among others. These factors provide a wide variety of climates: northeastern Brazil shows semiarid climates and in the central region of Brazil, tropical climate (or subtropical) is predominant.

There is need to analyze and understand the hydrological processes in agricultural areas and watersheds due to their impact on soil erosion and conservation measures. Of all regular climatic parameters, precipitation is the most changeable variable in time and space.

There are simple rainfall measures that can be used to provide information on variability, therefore on the climate state. These mainly include annual and monthly precipitation data of rainfall and averages, which can be used to assess rainfall seasonality, variability and the frequency of extreme events.

High percentages of total annual rainfall concentration in a few very rainy days can increase the risk of flooding and soil instability. In this work, a survey of the spatial and temporal patterns of daily and monthly rainfall concentration in southeast Brazil was conducted through a set of homogeneous daily rainfall data.

One of the most important aspects of climate variability that requires thorough investigation is the temporal distribution of rainfall and its historical changes. Precipitation is an important variable, since it gives rise to opposite phenomena such as drought and floods.

Several studies about rainfall variability have been performed worldwide using various statistical procedures. A significant decrease in the number of rainy days has been identified, as well as an increase in precipitation intensity values in many parts of the world, such as China [3] [4] [5] and America [6] . With regard to the Mediterranean area, several studies have been conducted to investigate the trends in annual and seasonal precipitation on a large scale [7] [8] [9] and for nations or whole regions,. [10] [11] [12] [13] Long-term rainfall records have been surveyed in Northern and Central Italy [14] [15] [16] , in Southern Italy [17] [18] [19] , in particular in the region of Calabria [20] [21] [22] .

Regarding the United States, the studies by [6] are worth mentioning, who found a 10% rainfall increase in the period from 1910 to 1995 and a positive trend in intense precipitation events (>90%). This increase is due to the increased frequency of days with precipitation, as well as an increase in its intensity.

Rainfall intensity, amount and pattern require detailed analysis, because these variables cause droughts or floods, likely to occur frequently in the region under study.

A higher rainfall concentration, represented by higher percentage of the total annual rainfall in some very rainy days, has the potential to cause floods and droughts. These phenomena have a considerable impact on water resources.

As consequences, rainfall amount and intensity can make the soil more vulnerable to erosion and increase instability. In particular, vulnerability to soil erosion will affect the growing conditions of plants and agricultural practices, changing the land use management [23] , and the instability of slopes can increase economic and life losses. According to [24] , the knowledge of the temporal distribution of heavy rainfalls allows assessing the amount of runoff and soil loss. Changes in the temporal rainfall distribution can also modify river systems, groundwater recharge, water availability, hydropower production [25] [26] [27] . For these reasons, it is important to analyze the statistical structure of rainfall rates based on the set of daily rainfall data.

Researchers from Europe and nearby geographical areas also conducted studies on daily rainfall. [28] [29] [30] found that 25% of the rainiest days repre- sented 75% of total annual rainfall volume and the high values of the daily rain concentration were located in the eastern region of the Iberian Peninsula.

Precipitation is one of the most important variables associated with monsoon anywhere in the world and the rainfall amount in a week or month varies widely. The monsoon season is well spatially organized on a large scale, but this is not true for smaller scales. Concentration indexes above 0.60 show one of the most characteristic traits of rain: its high concentration.

Rainfall analysis aimed at characterizing precipitation at different spatial and temporal scales is a widely discussed issue, mainly due to its involvement in hydrological processes and analysis of erosion and soil loss. In the current context, several authors have associated change in precipitation patterns to extreme weather events occurring more and more frequently in many parts of the world, such as China [31] [32] America [33] or in various areas of the Mediterranean [34] .

One must know the rainfall structure on a daily scale. [1] proposed a daily precipitation concentration index (CI), which has been applied in different regions with very different results. Thus, in the case of the Iberian Peninsula, spatial patterns of CI clearly showed two distinct areas: values ranging from 0.63 to 0.70 or more, in the peninsular regions of the eastern Mediterranean and lower values in other areas of Atlantic influence, where rain regularity is greater.

A subject that attracts attention in climatology studies is the guidance to establish monthly and annual averages, which makes daily (including hourly) information scarce. All these scales (daily, monthly and annual) have a great potential to characterize precipitation, as rain has a discrete pattern. Furthermore, the frequency distribution has daily values that are perfectly adjustable to negative exponential distribution [35] due to the existence of many days with precipitation of less than 1 mm and a few days with heavy rainfalls [1] .

The Concentration Index (CI) allows understanding the irregularity of daily rainfalls. It is an estimator of the degree of rainfall tolerance [1] and explains instability processes, formation of slopes [36] , danger of flooding and drought. CI is a synthetic indicator that summarizes all daily rainfall events.

Analysis of precipitation with daily resolution is a matter of great concern, anywhere in the world. This type of analysis is justified by the existence of serious environmental risks in the various regions of the planet, such as flooding and unstable soil resulting in high percentages of total annual rainfall falling on a limited number of very rainy days. Thus, the northern portion of southeastern Brazil has long periods of drought and uneven distribution of rainfall seasons.

To analyze the inter-annual rainfall distribution, [2] adapted an index from the geo-economic theory (industrial concentration) to quantify the relative distribution of rainfall patterns and estimate its seasonality [34] , which was called Precipitation Concentration Index.

The aim of this study was to determine the concentration of daily and monthly precipitation using methodology called daily and inter-annual concentration index developed by [1] first and [2] second.

2. Methodology

The study was conducted using meteorological data from the National Water Agency (ANA) for southeastern Brazil. The primary data set includes daily precipitation for the period from 1976 to 2010. The locations of weather stations are shown in Figure 1, comprising 120 stations.

To determine the relative impact of different daily precipitation classes and evaluate the weight of the greatest event on precipitation, it is necessary to analyze the percentage of accumulated precipitation (Y) contributed by the cumulative percentages of days (X) during the occurrence of Y [1] [32] [37] [38] [39] .

The concentration index proposed by [1] was used to determine the relative impact of different precipitation classes, e.g., more intense precipitation observed in the heterogeneity of daily precipitation [32] [34] [39] .

In a given time and place, the probability of small daily amounts of rainfall is greater than large daily amounts of rainfall. In other words, starting with the lowest class of daily rainfall, the absolute frequencies of daily precipitation exponentially decrease as it moves to the consecutive intervals [35] .

Based on the work of [34] [37] [38] [39] studied the cumulative percentage of precipitation (Pi) contributing to the cumulative percentages of days (Ni): 1) es-

Figure 1. Location of weather stations.

tablish the precipitation class limits (class interval of 5 mm), which could be from 1 to 10 mm; 2) count the number of days with rainfall interval that decreased for each class interval (i = 1, 2, ... n), calculating the associated amount of rainfall; 3) calculate the cumulative sum of output items based on step 2; 4) count the cumulative percentage of rainy days and the associated amount of rainfall based on step 3.

If the accumulated percentage of rainfall (Sum Pi) is a function of the cumulative percentage of rainy days (Sum Ni), an exponential curve is obtained and expressed by Sum(Ni) versus Sum(Pi) (Martin-Vide 2004):

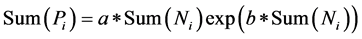
where a and b are regression analysis parameters.

The equation is called concentration curve or Lorenz curve (Figure 2), which has been widely used in many areas [40] . It should be noted that this curve is plotted with both axes ranging from 0 to 100%, giving a total area of 10,000. Thus, the Gini index (2S/10,000) was used to quantify the degree of concentration, where S is the area contained by the bisector quadrant and the Lorenz’s curve. The integral defined from the exponential curve between 0 and 100 is the area under the curve A’:

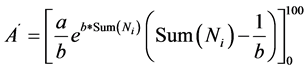
Based on areas A´ and S´ compressed by the curve, the equidistribution line and Ni(=100) is the difference between 5.000 and the value of A’. Coefficients a and A’ can be estimated by the least squares method. Then, the concentration index CI, resembling the Gini index, can be defined as:

Figure 2. Exponential curve of the cumulative number of precipitation days (Sum Ni) versus accumulated rainfall (Sum Pi). The solid black line is the equidistribution line.

The CI value is the S’ fraction and the area surface of the lower triangle is defined by equidistribution line. CI indicates the contribution of extreme precipitation for certain lengths of time.

Extreme rainfalls are associated with flooding; therefore, CI studies have scientific and practical merits, as they enable a better understanding of flood events in a given area.

If the concentration index is zero, there is complete precipitation uniformity and with CI = 1, total rainfall concentration occurs at a particular time.

The monthly rainfall heterogeneity was analyzed using the rainfall concentration index originally proposed by [2] and modified by [41] .

The modified index is expressed by:

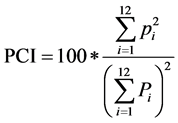
where pi is the amount of rainfall in the i-th month. The index was calculated for each rain gauge and for each year over the study period. As described by [2] , annual PCI values below 10 indicate uniform monthly rainfall distribution, while values from 11 to 20 denote seasonal rainfall distribution. Values above 20 correspond to climate with marked monthly contrasts in rain intensity.

Two different procedures can be adopted to assess this index: PCI can be estimated by the number of average monthly rainfall data or calculated from the year set and then as the average over several years. PCI related to the variation coefficient (VC) by the following equation:

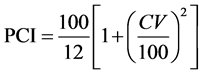
The values of all indexes used in this study were calculated using the R software through the precintcon function developed by [42] , where there are various input parameters such as the object to be analyzed and the period one wants to work, which should include the number of days or months to be grouped during the calculation of CI, PCI and SPI respectively. For example:

precintcon.ci.analysis (d1, d2, interval = 1), to calculate CI and where, in this case, the interval used for analysis is equal to one millimeter; precintcon.pci. analysis (d1), to calculate PCI.

The temporal trend of both indices (PCI and CI) was detected by the nonparametric Mann-Kendall test [43] [44] . The Mann-Kendall method can test the trends in time series (xk, k = 1, 2 ...... n) without the need for normality or linearity (Wang et al. 2008); being therefore highly recommended for general use by the World Meteorological Organization [45] and is widely used in detecting trends in hydrological series (e.g., [39] ). The statistical S test has zero mean and unit variance, given by the following equations:

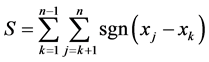
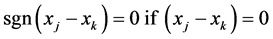
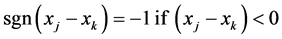
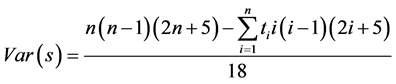
where n the number of data points; ti is the number of measure loops. In cases where the sample size n > 10, the statistical standard (Z) for a tailed test is formulated as:

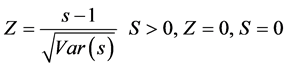
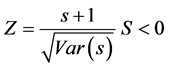
The 95% significance level, the null hypothesis of no trend is rejected if |Z| > 1.96. For the 95% significance level, the null hypothesis of no trend is rejected if |Z| > 1.64.

3. Results and Discussion

Figure 3 shows that the daily concentration index values did not exceed 0.60, which is a threshold between low and high CI, indicating that there is no marked concentration values, but there is a clear gradient towards the northern/nor- theastern region, i.e., the rains are more concentrated towards the Drought Polygon (north of the study area). This spatial pattern is very consistent from a climatic and geographical point of view.

Figure 3. Concentration Index lines (CI) for 5 mm classes.

The values found for central Chile, for example, vary between 0.47 and 0.75. More than 36 of the 56 meteorological stations (64%) showed CI 0.59, which is consistent with values of the index for the Iberian Peninsula. However, 36% of the stations are under this threshold.

The daily precipitation concentration calculated by the CI confirmed that the southern and central parts of Chile have values similar to those of the Iberian Peninsula, with high values of this index for Mediterranean climates and low CI for rainy oceanic climates. In the Southeast Region of Brazil, this does not occur because values are below 0.60.

The spatial distribution of the Monthly Concentration Index (PCI) (Figure 4) shows a gradient from south (southwestern region) to north (northeastern region). This index was used to classify three basic regions: irregular distribution (>40), highly seasonal (30 - 40) and seasonal (<30). Regarding the southeastern region, no value exceeded 20, so it could be inferred that rain is seasonal.

In Chile, for example, according to Sarricolea and Martin-Vide (2012), values of this index ranging from 40 (northern region) to 25 (southern region) could be observed, characterizing that to the north, in the Coquimbo region, rainfall is distributed only over one month, while in the transition region (Coquimbo and Valparaiso), this precipitation is quarterly and during winter. Farther south, from the metropolitan area to Curicó, precipitation extends from May to September (five months). This pattern is very different from the southeastern region of Brazil.

Figures 5-8 show the relationship between CI and the precipitation percentage of rainy days to 10%, 20%, 30% and 50%, based on the rainfall stations analyzed. It was possible to determine the percentage of total rainfall, corresponding

Figure 4. Monthly Concentration Index (PCI) in southeastern Brazil.

Figure 5. 10% of rainfall in the area according to CI. R2 = 0.89 (PP-10% = 129.4*CI − 26.1) significant: The linear coefficient of determination, R2 of 10% of the rainfall).

Figure 6. 20% of rainfall in the area according to CI. R2 = 0.75 (PP-20% = 109.2*CI − 0.024) significant: The linear coefficient of determination, R2 of 20% of the rainfall).

Figure 7. 30% of rainfall in the area according to CI. R2 = 0.66 (PP-30% = 93.05*CI + 18.6) (significant: The linear coefficient of determination, R2 of 30% of the rainfall).

Figure 8. 50% of rainfall in the area according to CI. R2 = 0.93 (PP-50% = 61.38*CI + 48.77) (significant: The linear coefficient of determination, R2 of 50% of the rainfall).

to a certain percentage of the number of rainy days. This shows that the higher the percentage of rainfall in rainy days corresponding to a weather station, the higher the CI.

The linear determination coefficient (R2) is equal to 0.93% for 50% of the rainfall that occurred in the region. In the other relationships of CI with the proportions of days with rainfall, the value ranges from 0.66 to 0.89. Thus, the heterogeneity of daily precipitation within a year can be better accounted for by the percentage of rainfall that contributed with 50% of the rainiest days in the study area.

Table 1 shows rainfalls that contributed with 15 and 25% of the rainiest days for the series analyzed. This table shows that in 15% of rainy days, rainfall occurred between 49.5 to 56.8 mm and in 25%, rainfalls occurred between 68.8 to 61.9 mm.

In general, according to Martin-Vide (2004), values above 0.61 for CI mean that 70% of the total precipitation contributes with 25% of the rainy days.

Table 1 shows the PCI values at each station and its standard statistics (ZPCI), as well as CI and its standardized statistics, the trend tested by the Mann-Kendall method. It was observed through the absolute values of ZPCI (Table 1) that there are values smaller than 1.64% for 90% significance level, which means that the trends are not significant for these stations; however, there are some in which absolute values are greater than 1.64. In this case, through this method, it could be concluded that there is a tendency. The same could be said for the absolute ZCI values. Values marked with the symbol (*) indicates that there are significant trends for the 90% significance level.

However, it was observed that these non-significant trends in PCI are negative for almost all of the analyzed series. The suggestion of positive trends implies a tendency for increased annual concentration of total rainfall for the summer, considered the rainy season. It is not that what occurs in this region, based on PCI values analyzed.

Table 1. Values of a and b coefficients of the exponential curve, determination coefficients (R2), CI and ZCI, PCI and ZPCI and the percentage of rainfall contributed by 15 and 25 of the rainiest days for some weather stations during the study period in southeastern Brazil.

(*) Represents a significant trend tested at 90% significant level.

The CI values for some rainfall series were estimated in terms of values of regression coefficients a and b in equations Sum(Pi)and A’.

The positive trends in the case of CI (ZCI) indicates extreme inequality of rainfall distribution and increased chance of occurrences of droughts and floods, which leads to the need of thinking about influence strategies for prevention of flooding or water use in the study area.

4. Conclusions

The analysis of the degree of rainfall concentration throughout the year is extremely important due to its high impact on environmental phenomena such as floods and droughts. In this study, the rainfall distribution on daily and monthly scales in southeastern Brazil was determined. The precipitation concentration index (PCI) was used to evaluate the rainfall seasonality and the concentration index (CI) was used to evaluate the weight of the greatest daily events relative to the total amount of precipitation.

The PCI results showed marked rainfall seasonality in the study area. PCI and CI values were not high within the southeastern region compared to those obtained in Chile and Spain.

The results also show that a large percentage of precipitation is provided by the highest quartile of the rainy days. Daily rainfall heterogeneity within one year can be best explained by the percentage of rainfall that contributed with 50% of rainy days in the study area.

Cite this paper

Nery, J.T., Carfan, A.C. and Martin-Vide, J. (2017) Analysis of Rain Variability Using the Daily and Monthly Concentration Indexes in Southeastern Brazil. Atmospheric and Climate Sciences, 7, 176- 190. https://doi.org/10.4236/acs.2017.72013

References

  1. 1. Martin-Vide, J. (2004) Spatial Distribution of a Daily Precipitation Concentration Index in Peninsular Spain. International Journal of Climatology, 24, 959-971.
    https://doi.org/10.1002/joc.1030

  2. 2. Oliver, J.E. (1980) Monthly Precipitation Distribution: A Comparative Index. Professional Geographer, 32, 300-309.
    https://doi.org/10.1111/j.0033-0124.1980.00300.x

  3. 3. Ren, G.Y., Wu, H. and Chen, Z.H. (2000) Spatial Patterns of Change Trend in Rainfall of China. Quarterly Journal of Applied Meteorology, 11, 322-330.

  4. 4. Gong, D.Y. and Ho, C.H. (2002) Shift in the Summer Rainfall over the Yangtze River Valley in the Late 1970s. Geophysical Research Letters, 29, 14-36.
    https://doi.org/10.1029/2001GL014523

  5. 5. Zhai, P.M., Zhang, X.B., Wan, H. and Pan, X.H. (2005) Trends in Total Precipitation and Frequency of Daily Precipitation Extremes over China. Journal of Climatology, 18, 1096-1108.
    https://doi.org/10.1175/JCLI-3318.1

  6. 6. Karl, T.R., Knight R.W., Easterling, D.R. and Quayle, R.G. (1996) Indices of Climate Change. American Meteorological Society, 77, 279-292.
    https://doi.org/10.1175/1520-0477(1996)077<0279:IOCCFT>2.0.CO;2

  7. 7. Kutiel, H., Maheras, P. and Guika, S. (1996) Circulation and Extreme Rainfall Conditions in the Eastern Mediterranean during the Last Century. International Journal of Climatology, 16, 73-92.
    https://doi.org/10.1002/(SICI)1097-0088(199601)16:1<73::AID-JOC997>3.0.CO;2-G

  8. 8. Piervitali, E., Colacino, M. and Conte, M. (1998) Rainfall over the Central-Western Mediterranean Basin in the Period 1951-1995, Part I: Precipitation Trends. Nuovo Cimento, 21, 331-344.

  9. 9. Xoplaki, E., Luterbacher, J. and González-Rouco, J.F. (2006) Mediterranean Summer Temperature and Winter Precipitation, Large-Scale Dynamics, Trends. Nuovo Cimento, 29, 45-54.

  10. 10. Amanatidis, G.T., Paliatsos, A.G., Repapis, C.C. and Barttzis, J.G. (1993) Decreasing Precipitation Trend in the Marathon Area, Greece. International Journal of Climatology, 13, 191-201.
    https://doi.org/10.1002/joc.3370130205

  11. 11. De Luis, M., Raventos, J., Gongález-Hidalgo, J.C., Sánchez, J.R. and Cortina, J. (2000) Spatial Analysis of Rainfall Trends in the Region of Valencia (East of Spain). International Journal of Climatology, 20, 1451-1469.
    https://doi.org/10.1002/1097-0088(200010)20:12<1451::AID-JOC547>3.0.CO;2-0

  12. 12. Feidas, H., Noulopoulo, Ch., Makkrogiannis, T. and Bora-Senta, E. (2007) Trend Analysis of Precipitation Time Series in Greece and Their Relationship with Circulation Using Surface and Satellite Data: 1955-2001. Theoretical and Applied Climatology, 87, 155-177.
    https://doi.org/10.1007/s00704-006-0200-5

  13. 13. Del Rio, S., Herrero, L., Fraile, R. and Penas, A.P. (2011) Spatial Distribution of Recent Rainfall Trends in Spain (1961-2006). International Journal of Climatology, 31, 656-667.
    https://doi.org/10.1002/joc.2111

  14. 14. Montanari, A., Rosso, R. and Taqqu, M.S. (1996) Some Long-Run Properties of Rainfall Records in Italy. Journal of Geophysical Research, 101, 431-438.
    https://doi.org/10.1029/96JD02512

  15. 15. De Michele, C., Montanari, A. and Rosso, R. (1998) The Effect of Non-Stationarity on the Evaluation of Critical Design Storms. Water Science and Technology, 37, 187-193.
    https://doi.org/10.1016/S0273-1223(98)00332-1

  16. 16. Brunetti, M., Nanni, T., Maugeri, M., Auer, I., Boehm, R. and Schoerer, W. (2006) Precipitation Variability and Changes in the Greater Alpine Region over the 1800-2003 Period. Journal of Geophysical Research Atmospheres, 111, D11107.

  17. 17. Palmieri, S., Siani, A.M. and D’Agostino, A. (1991) Climate Fluctuations and Trends in Italy within the Last Hundred Years. Annals of Geophysics, 9, 769-776.

  18. 18. Brunetti, M., Buffoni, L., Mangianti, F., Maugeri, M. and Nanni, T. (2004) Temperature, Precipitation and Extreme Events during the Last Century in Italy. Global Planet Change, 40, 141-149.
    https://doi.org/10.1016/S0921-8181(03)00104-8

  19. 19. Cotecchia, V., Casarano, D. and Polemio, M. (2004) Characterization of Rainfall Trend and Drought Periods in Southern Italy from 1821 to 2001. Proceedings of 1st Italian-Russian Workshop New Trends in Hydrology, CNR Publications 2823, Rende, 24-26 September 2004, 139-150.

  20. 20. Coscarelli, R., Gaudio, R. and Caloier, T. (2004) Climatic Trends: An Investigation for a Calabrian Basin (Southern Italy). Proceedings of the International Symposium the Basis of Civilization, Water Science? IAHS Publication, No. 286, Rome, 3-6 December 2003, 255-266.

  21. 21. Ferrari, E. and Terranova, O. (2004) Non-Parametric Detection of Trends and Change Point Years in Monthly and Annual Rainfalls. In: Gaudio, R., Ed., Proceedings of 1st Italian-Russian Workshop New Trends in Hydrology, CNR Publications 2823, Rende, 24-26 September 2004, 177-188.

  22. 22. Buttafuoco, G., Caloiero, T. and Coscarelli, R. (2011) Spatial and Temporal Patterns of the Mean Annual Precipitation at Decadal Time Scale in Southern Italy (Calabria Region). Theoretical and Applied Climatology, 105, 431-444.
    https://doi.org/10.1007/s00704-011-0398-8

  23. 23. Scholz, G., Quinton, J.N. and Strauss, P. (2008) Soil Erosion from Sugar Beet in Central Europe in Response to Climate Change Induced Seasonal Precipitation Variations. Catena, 72, 91-105.
    https://doi.org/10.1016/j.catena.2007.04.005

  24. 24. Klik, A. and Truman, C.C. (2003) What Is a Typical Rainstorm? In: Gabriels, D. and Cornelis, W., Eds., Proceedings of the International Symposium, 25 Years of Assessment of Erosion, Ghent, 22-26 September 2003, 93-98.

  25. 25. Aguado, E., Cayan, D., Riddle, L. and Roos, M. (1992) Climatic Fluctuations and the Timing of West-Coast Streamflow. Journal of Climatology, 5, 1468-1483.
    https://doi.org/10.1175/1520-0442(1992)005<1468:CFATTO>2.0.CO;2

  26. 26. Paredes, D., Trigo, R.M., Garcia-Herrera, R. and Franco-Trigo, I. (2006) Understanding Precipitation Changes in Iberia in Early Spring: Weather Typing and Storm Tracking Approaches. Journal of Hydrometeor, 7, 101-113.
    https://doi.org/10.1175/JHM472.1

  27. 27. López-Moreno, J.I., Vicente, S., Gimeno, L. and Nieto, R. (2009) Stability of the Seasonal Distribution of Precipitation in the Mediterranean Region: Observations Since 1950 and Projections for the 21st Century. Geophysical Research Letters, 36, L10703.
    https://doi.org/10.1029/2009GL037956

  28. 28. Sánchez-Lorenzo, A. and Martin-Vide, J. (2006) Distribución espacial de la concentración pluviométrica diaria en la Península Ibérica. Proceedings 5a Asamblea Hispano Portuguesa de Geodesia y Geofísica, sesión Climatología y Cambio Climático, Sevilla, 4 p.

  29. 29. Benhamrouche, A. and Martin-Vide, J. (2011) Distribución Espacial de la Concentración Diaria de La Precipitación en la Provincia de Alicante. Investigaciones Geográficas, 56, 113-129. (In Spanish)
    https://doi.org/10.14198/INGEO2011.56.06

  30. 30. Benhamrouche, A. and Martin-Vide, J. (2012) Avances metodológicos en el análisis de La concentración diaria de la precipitación en la Espana peninsular. Anales de Geografía, 32, 11-27.

  31. 31. Zhang, Q., Xu, C.Y., Marco, G., Chen, Y.P. and Liu, C.L. (2009) Changing Properties of Precipitation Concentration in the Pearl River Basin, China. Stochastic Environmental Research and Risk Assessment, 23, 377-385.
    https://doi.org/10.1007/s00477-008-0225-7

  32. 32. Li, X., Jiang, F., Li, L. and Wang, G. (2010) Spatial and Temporal Variability of Precipitation Concentration Index, Concentration Degree and Concentration Period in Xinjiang, China. International Journal of Climatology, Published Online, 31, 1679-1693.
    https://doi.org/10.1002/joc.2181

  33. 33. Karl, T.R. and Knight, R.W. (1998) Secular Trends of Precipitation Amount, Frequency, and Intensity in the United States. Bulletin of the American Meteorological Society, 79, 231-241.
    https://doi.org/10.1175/1520-0477(1998)079<0231:STOPAF>2.0.CO;2

  34. 34. Coscarelli, R. and Caloiero, T. (2012) Analysis of Daily and Monthly Rainfall Concentration in Southern Italy. Journal of Hydrology, 416-417, 145-156.
    https://doi.org/10.1016/j.jhydrol.2011.11.047

  35. 35. Brooks, C.E.P. and Carruthers, N. (1953) Handbooks of Statistical Methods in Meteorology. Meteorological Office, London.

  36. 36. Zubieta, R. and Saavedra, M. (2009) Spatial Distribution of a Daily Precipitation Concentration Index in Central Andes of Peru: Mantaro River Valley. TECNIA, 19, 13-22.

  37. 37. Riehl, H. (1949) Some Aspects of Hawaiian Rainfall. Bulletin American Meteorological Society , 3, 176-187.

  38. 38. Olascoaga, M.J. (1950) Some Aspects of Argentine Rainfall. Tellus, 2, 312-318.

  39. 39. Zhang, Q., Liu, C.L., Xu, C.Y., Xu, Y.P. and Jiang, T. (2006) Observed Trends of Annual Maximum Water Level and Streamflow during Past 130 Years in the Yangtze River Basin, China. Journal of Hydrology, 324, 255-265.

  40. 40. Shaw, G. and Wheeler, D. (1994) Statistical Techniques in Geographical Analysis. Halsted Press, New York.

  41. 41. De Luis, M., González-Hidalgo, J.C., Raventós, J., Sánchez, J.R. and Cortina, J. (1997) Distribución espacial de la concentración y agresividad de la lluvia en el territorio de la comunidad valenciana. Cuaternario y Geomorfología, 11, 33-44.

  42. 42. Povoa, L.V. and Nery, J.T. (2016) Precintcon: Precipitation Intensity, Concentration and Anomaly Analysis. R Package Version 2.3.0. Comprehensive R Archive Network, Austria.
    https://CRAN.R-project.org/package=precintcon

  43. 43. Kendall, M.G. (1962) Rank Correlation Methods. Hafner Publishing Company, New York.

  44. 44. Mann, H.B. (1945) Nonparametric Tests against Trend. Econometrica, 13, 245-259.
    https://doi.org/10.2307/1907187

  45. 45. Mitchell, J.M., Dzeerdzeevskii, B., Flohn, H., Hofmeyr, W.L., Lamb, H.H., Rao, K.N. and Wallén, C.C. (1966) Climate Change. Technical Note No. 79, World Meteorological Organization, Geneva.

上一篇:Assessment of Regional Climate 下一篇:Conditions Supporting Funnel C

我要分享到：